|
|
|
The field of nanophotonics witnesses a sort of golden age, where many new fields, such as plasmonics, metamaterials, transformation optics, have risen recently, leading to a wealth of new directions of research. The story started more than 20 years ago, when new artificial structures were imagined that could exhibit a photonic bandgap. These structures were called photonic crystals.1 They have carried a lot of hope on the possibility of molding the flow of light. It was indeed soon recognized that they could go way beyond the bandgap and that, in fact, they had a very rich band structure that allowed for control over the propagation of light itself, inside the photonic crystal. This has led to such effects as ultrarefraction, slow light, control of second harmonic emission, gradient photonic crystals, and negative refraction. Somehow, this wealth of properties has slowed down researches with the original quantum flavor of photonic crystals, at least as it appeared in the work of Sajeev John, which were seen really as devices able to control the Purcell effect. This was, for instance the case for the idea of realizing a laser cavity with a very low threshold. This aspect has shown a renewed interest recently.2 If the history of nanophotonics is followed further, the concept of metamaterials is encountered.3 It is somehow a generalization of photonic crystals, in that it is artificial periodic devices whose basic cell can be, however, very complicated. The point at issue is to look at these structures from the point of view of the effective properties. That is to envision these structures when they are illuminated by an incident plane wave whose wavelength is larger than twice the period. In that situation, it can be hoped to describe the metamaterials by homogeneous constitutive relations. It is what happens in matter, at a much lower scale: for wavelengths of, say, the visible spectrum, matter, despite its discrete, granular aspect, appears as if it were homogeneous with permittivity and permeability tensors describing how it interacts with light at a macroscopic level. The point at issue is of course to be able to derive these macroscopic properties from the microscopic ones. This comes under homogenization theory.4, 5, 6 Homogenization theory is quite an old subject. In the field of electromagnetics, it occupied people by the end of the 19th century already, and during the 20th century it was applied to mechanics (with the theory of thin plates) as it spreads towards the community of mathematicians. It is nowadays a hot topic, precisely due to the interest in the effective properties of metamaterials. Here a parenthesis should be opened on the lack of communication between physicists and mathematicians. If one browses the now vast literature of physics on the effective properties of metamaterials, one notes that there is almost no citation of any of the numerous mathematicians involved in the rigorous treatment of the theory. Let us cite the french school with Lions, Bensoussan, Tartar, Murat, Allaire, Bouchitté, Villani, the russian school: Jikov, Oleinik, Kozlov, the italian school: De Giorgi, Butazzo, the american school: Papanicolaou, Vogelius and so on, many names being omitted. Despite the fact that many excellent books were written,7 it seems that very few physicists are aware of the very existence of this theory.8 However, the physics literature sometimes provide some very useful and accurate formulas.9, 10 Certainly it would be a major advance to come up with a synthesis of both approaches. Anyway, the point at issue here is that metamaterials are for the moment purely classical structure: they are made of wires and metallic loops, dielectric or metallic spheres, or nanorods. They do not belong for the moment to the quantum world, although it should be noted that the properties of photonic structures in which quantum systems are embedded have already been explored.11 The point at issue in what could be called “quantum metamaterials” would be to use quantum-in-essence systems (e.g., molecules, quantum dots, cold atoms, Josephson junctions) embedded in a photonic structure in order to tailor the effective properties. Here “effective properties” could mean not only electromagnetic constitutive relations, but, more generally, emergent collective behaviors: in that respect superconductors are somehow metamaterials! For instance it was already suggested by Rakhmanov12 (using the term quantum metamaterials) to use arrays of Josephson junctions to exploit quantum coherence in metamaterials. More generally, it could be possible to reproduce the full range of atomic spectroscopy spectra. As compared to what happens in the basic elements of metamaterials (i.e., open cavity resonances), what would be most interesting would be to be able to address the quantum dynamics that allows for transitions between levels (inversion of population), the entanglement between states (quantum information applications), the tunability of the effective properties. Let us give an example as a first step: consider an array of nanowires such as that depicted in Fig. 1. They can be put into periodic positions with some lattice symmetry, so as to produce a photonic bandgap. It is possible to grow inside the wire a quantum dot with an electric dipole perpendicular to the axis of the wire. By pumping this medium it is possible to make a transition from a conducting state to a bandgap. My group has found that, by pumping this medium, it is possible to make a transition from a conducting state to a bandgap.13 Fig. 1Sketch of a quantum metamaterials based on nanowires with quantum dots inserted. The propagation of the probe beam can be tuned by the pumped beam. 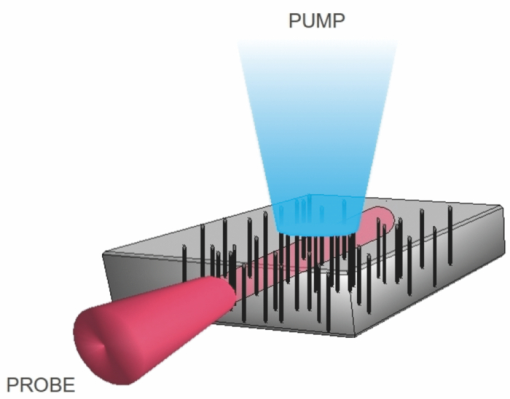 Finally, I would like to sketch an interesting connection between cold atoms and metamaterials. The limitations of the model of an artificial atom for the description of quantum dots have been analyzed14 and the existence of phonons affects the emission properties. I would like to stress that periodic arrays of cold atoms could be an ideal model of solid-state quantum metamaterials, i.e., quantum dots embedded in a photonic crystal (or a classical metamaterial). Indeed, quantum dots are never alike and the size dispersion can make collective effects disappear but atoms are all identical. Somehow, ultracold gases are already considered as quantum metamaterials: they allow to reproduce the many-body physics of solid-state physics.15 AcknowledgmentsI thank G. Cassabois and M. Antezza for enlightening discussions. The financial support of the Institut Universitaire de France is gratefully acknowledged. ReferencesJ. D. Joannopoulos, S. G. Johnson, J. N. Winn, and
R. D. Meade, Photonic Crystals: Molding the Flow of Light, 2nd ed.Princeton University Press, Princeton, NJ
(2008). Google Scholar
Y. Kurosaka, S. Iwahashi, Y. Liang, K. Sakai, E. Miyai, W. Kunishi, D. Ohnishi and S. Noda,
“On-chip beam-steering photonic-crystal lasers,”
Nat. Photon., 4 447
–450
(2010). http://dx.doi.org/10.1038/nphoton.2010.118 Google Scholar
S. A. Ramakrishna,
“Physics of negative refractive index materials,”
Rep. Prog. Phys., 68 449
–521
(2005). http://dx.doi.org/10.1088/0034-4885/68/2/R06 Google Scholar
D. Felbacq and G. Bouchitte,
“Homogenization of a set of parallel fibres,”
Waves Random Complex Media, 7 245
–256
(1997). http://dx.doi.org/10.1088/0959-7174/7/2/006 Google Scholar
D. Felbacq and G. Bouchitte,
“Theory of mesoscopic magnetism in photonic crystals,”
Phys. Rev. Lett., 94 183902
(2005). http://dx.doi.org/10.1103/PhysRevLett.94.183902 Google Scholar
G. Bouchitte and D. Felbacq,
“Homogenization of a wire photonic crystal: The case of small volume fraction,”
SIAM J. Appl. Math., 66 2061
–2084
(2006). http://dx.doi.org/10.1137/050633147 Google Scholar
V. V. Jikov, S. M. Kozlov, and O. A. Olenik, Homogenization of Differential Operators and Integral Functionals, Springer, Berlin(1994). Google Scholar
C. R. Simovski,
“On electromagnetic characterization and homogenization of nanostructured metamaterials,”
J. Opt., 13 013001
(2011). http://dx.doi.org/10.1088/2040-8978/13/1/013001 Google Scholar
T. C. Choy, Effective Medium Theory, Clarendon Press, Oxford
(1999). Google Scholar
Introduction to Complex Mediums for Optics and Electromagnetics, SPIE Press, Bellingham, WA
(2003). Google Scholar
P. Ginzburg and M. Orenstein,
“Metal-free quantum-based metamaterial for surface plasmon polariton guiding with amplification,”
J. Appl. Phys., 104 063513
(2008). http://dx.doi.org/10.1063/1.2978208 Google Scholar
A. Rakhmanov, A. Zagoskin, S. Saveliev, and F. Nori,
“Quantum metamaterials: Electromagnetic waves in a Josephson qubit line,”
Phys. Rev. B, 77 144507
(2008). http://dx.doi.org/10.1103/PhysRevB.77.144507 Google Scholar
D. Felbacq and G. Cassaboi, Google Scholar
G. Cassabois and R. Ferreira,
“Dephasing processes in a single semiconductor quantum dot,”
C. R. Phys., 9 830
–839
(2008). http://dx.doi.org/10.1016/j.crhy.2008.10.009 Google Scholar
I. Bloch, J. Dalibard, and W. Zwerger,
“Many-body physics with ultracold gases,”
Rev. Mod. Phys., 80 885
–964
(2008). http://dx.doi.org/10.1103/RevModPhys.80.885 Google Scholar
|


