|
|
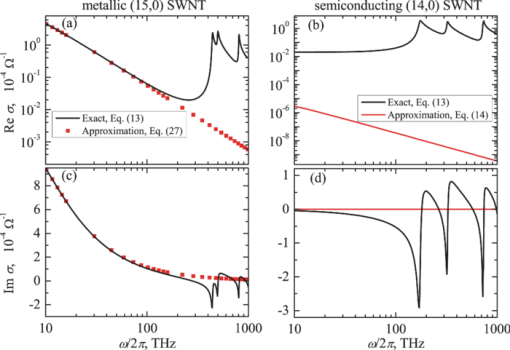
1.IntroductionPeculiar electronic1 and optical properties2 of carbon nanotubes (CNTs) stimulate intensive studies of their electromagnetic response. Recently, the problem of the electromagnetic field diffraction by isolated CNTs,3, 4, 5 bundles, and composites6, 7 containing CNTs received a lot of attention due to the potentiality of CNT-based materials for the effective manipulation of electromagnetic fields in the megahertz, gigahertz, and terahertz frequency ranges. The scattering of the electric near-fields by CNTs8, 9 has important applications in the near-field optical microscopy and spectroscopy with the CNT-based probes. Theoretical consideration of these problems requires knowledge of the linear surface conductivity of CNTs. Though the expressions for the conductivity of a single-wall carbon nanotube (SWNT) were previously obtained in Ref. 10 I feel the necessity to present the results of Ref. 10 for the general audience. The main idea of the article is to explain the method of the SWNT surface conductivity calculation and to provide the reader with the ready-to-use expressions for the conductivity. For this purpose I use the density matrix formalism that was applied previously11, 12, 13 for studying the nonlinear optical properties of SWNTs. The outline of the paper is as follows: equations of motions for the density matrix are discussed in Sec. 2, and the expressions for the SWNT conductivity are presented in Sec. 3. The consideration is restricted to the case of achiral zigzag (m, 0) SWNTs and armchair (m, m) SWNTs. 2.Equations of Motion for the Density Matrix of the π-Electron Subsystem in an SWNTLet us consider an infinitely long achiral SWNT of a cross-sectional radius Rcn aligned parallel to the z-axis of the Cartesian coordinate system. Suppose that the SWNT is exposed to the plane monochromatic electromagnetic wave propagating normally to the SWNT axis and the electric field of the wave is polarized along the SWNT axis. As the typical SWNT radius (of order of 1 nm) is small compared to the electromagnetic field wavelength up to the x ray frequency region we can neglect the space inhomogeneity of the electric field on the SWNT surface and present it as follows: Eq. 1[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{equation} \mathbf {E}(t) =\mathbf {e}_z E(t) = \mathbf {e}_z( E_0 e^{-i\omega t} + {\rm c.c}.), \end{equation} \end{document}The state of the π-electron subsystem in the SWNT can be characterized by the single-electron density matrix ραβ(t, pz, s), where α, β = c, v, indices c, v correspond to the conduction and valence bands, respectively, and pz is the projection of the electron quasimomentum on the SWNT axis. Due to the quantization of the electron quasimomentum component normal to the SWNT axis1 both the valence and the conduction bands of zigzag (m, 0) and armchair (m, m) SWNTs are split on m sub-bands enumerated by an integer index s = 1, …, m. The equations of motion for the π-electron density matrix of the SWNT exposed to the electromagnetic field Eq. 1 has the following form11, 12 Eq. 2[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \hspace*{-12pt}\frac{\partial \rho (t,p_z,s)}{\partial t} + e \,E(t) \displaystyle\frac{\partial \rho (t,p_z,s)}{\partial p_z} &=& -\frac{\rho (t,p_z,s)-\rho ^{eq}(p_z,s)}{\tau _1} \nonumber \\ &&+\displaystyle \frac{2 i\,e}{\hbar } \,E(t) R_{c v}(p_z,s) [\rho _{cv}^*(t,p_z,s)-\rho _{cv}(t,p_z,s)]\,, \end{eqnarray} \end{document}Eq. 3[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \frac{\partial \rho _{cv}(t,p_z,s)}{\partial t} +\, e \,E(t)\displaystyle\frac{\partial \rho _{cv}(t,p_z,s)}{\partial p_z}& =& - i\omega _{cv}(p_z,s) \rho _{cv}(t,p_z,s) - \frac{\rho _{cv}(t,p_z,s)}{\tau _2} \nonumber \\ &&-\displaystyle\frac{i\,e}{\hbar } \, E(t) R_{c v}(p_z,s)\rho (t,p_z,s)\,, \end{eqnarray} \end{document}Equations 2, 3 take into account both intraband and direct interband transitions of π electrons. Contribution of π electrons indirect interband transitions to the electromagnetic response of an achiral SWNT can be neglected. As no assumption was made about the smallness of the electric field amplitude E0 while deriving Eqs. 2, 3, these equations can describe interaction between the SWNT and the electromagnetic field both in linear10 and non-linear regimes.11, 12, 13 As the single-electron approximation was used to obtain Eqs. 2, 3, these equations can not account for the influence of the excitons on the electromagnetic properties of the SWNTs, though this influence can be essential in the optical frequency range.14 We are interested in the linear electromagnetic response of the SWNT. Using the perturbation theory we seek for the solution of Eqs. 2, 3 in the form: Eq. 4[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{equation} \rho (t,p_z,s)=\rho ^{eq}(p_z,s)+\lambda \rho ^{(1)}(t,p_z,s), \quad \rho _{cv}(t,p_z,s)=\lambda \rho _{cv}^{(1)}(t,p_z,s), \end{equation} \end{document}Eq. 5[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \frac{\partial \rho ^{(1)}(t,p_z,s)}{\partial t}+\frac{\rho ^{(1)}(t,p_z,s)}{\tau _1} &=- e \,E(t) \displaystyle\frac{\partial \rho ^{eq}(p_z,s)}{\partial p_z}\,, \end{eqnarray} \end{document}Eq. 6[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \frac{\partial \rho _{cv}^{(1)}(t,p_z,s)}{\partial t}+\left[i\omega _{cv}(p_z,s)+\frac{1}{\tau _2} \right] \rho _{cv}^{(1)}(t,p_z,s) &= -\displaystyle\frac{i e}{\hbar } \, E(t) R_{c v}(p_z,s)\rho ^{eq}(p_z,s)\,, \end{eqnarray} \end{document}Eq. 7[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \rho ^{(1)}(t,p_z,s) &= \tilde{\rho }^{(1)}(\omega ,p_z,s) E_0 e^{-i\omega t}+{\rm c.c.}, \end{eqnarray} \end{document}Eq. 8[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \rho ^{(1)}_{cv}(t,p_z,s) &= \tilde{\rho }^{(-)}_{cv}(\omega ,p_z,s) E_0 e^{-i\omega t}+\tilde{\rho }^{(+)}_{cv}(\omega ,p_z,s) E_0 e^{i\omega t}. \end{eqnarray} \end{document}3.SWNT ConductivityCurrent density induced in an achiral SWNT by the electromagnetic field has the following form:11, 12 Eq. 11[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} j(t) &=&\frac{2 e}{(2 \pi \hbar )^2} \frac{\hbar }{R_{cn}} \sum _{s=1}^m \displaystyle\int \limits _{-a}^{a} \left\lbrace \frac{\partial \mathcal {E}_c(p_z,s)}{\partial p_z} \rho ^{(1)}(t,p_z,s)\right. \nonumber \\ &&+ \left. i\, \omega _{c v}(p_z,s) R_{c v}(p_z,s) \left[\rho _{cv}^{(1)*}(t,p_z,s)-\rho _{cv}^{(1)}(t,p_z,s)\right]\right\rbrace d p_z, \end{eqnarray} \end{document}Eq. 12[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{equation} j(t) = \sigma (\omega ) E_0 e^{-i\omega t} + {\rm c.c.}, \end{equation} \end{document}Eq. 13[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{equation} \sigma (\omega ) = \sigma _1(\omega ) + \sigma _2(\omega ) \end{equation} \end{document}Eq. 14[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \sigma _1 & = -\displaystyle\frac{i e^2}{2 \pi ^2 R_{cn} \hbar (\omega + i/\tau _1)} \sum _{s=1}^m\int \limits _{-a}^{a} \frac{\partial \mathcal {E}_c(p_z,s)}{\partial p_z}\frac{\partial \rho ^{eq}(p_z,s)}{\partial p_z} \, dp_z, \end{eqnarray} \end{document}Eq. 15[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \sigma _2 & = \displaystyle\frac{i e^2}{ \pi ^2 R_{cn} \hbar ^2 } \sum _{s=1}^m\int \limits _{-a}^{a} \frac{ \omega _{cv}(p_z,s) R_{cv}^2(p_z,s) \rho ^{eq}(p_z,s) (\omega + i/\tau _2)}{\omega _{cv}^2(p_z,s)-(\omega +i/\tau _2)^2}\, dp_z. \end{eqnarray} \end{document}Define the functions that are present in Eqs. 14, 15. The frequency of the electron interband transitions ωcv and equilibrium inversion ρeq are related to the dispersion law of π electrons in the following way: Eq. 16[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \omega _{cv} (p_z,s) &= \displaystyle\frac{\mathcal {E}_c(p_z,s)-\mathcal {E}_v(p_z,s)}{\hbar }\,, \end{eqnarray} \end{document}Eq. 17[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \rho ^{eq}(p_z,s) & = F\left[\mathcal {E}_c(p_z,s)\right] - F \left[\mathcal {E}_v(p_z,s)\right], \end{eqnarray} \end{document}Eq. 18[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{equation} F(\mathcal {E}) = \left[1+\mathrm{exp}\left(\frac{\mathcal {E}}{k_B T}\right)\right]^{-1} \end{equation} \end{document}Eq. 19[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \mathcal {E}_{c,v}(p_z,s) &=\pm \gamma _{0}\left[1+4\cos \left(\displaystyle\frac{3 b p_{z}}{2\hbar }\right)\cos \left(\displaystyle\frac{\pi s}{m}\right)+4\cos ^{2}\left(\displaystyle\frac{\pi s}{m}\right)\right]^{1/2}\,, \end{eqnarray} \end{document}Eq. 20[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} R_{cv}(p_{z},s) &=-\displaystyle\frac{b\gamma _{0}^{2}}{2\mathcal {E} _{c}^{2}(p_{z},s)}\left[1+\cos \left(\frac{3 b p_{z}}{2\hbar }\right) \cos \left(\frac{\pi s}{m}\right) -2\cos ^{2}\left(\frac{\pi s}{m}\right)\right] \,, \end{eqnarray} \end{document}Eq. 21[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} R_{cn} & = \displaystyle\frac{\sqrt{3} b m}{2\pi }, \quad a = \frac{2\pi \hbar }{3 b}, \end{eqnarray} \end{document}Eq. 22[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \mathcal {E}_{c,v}(p_{z},s) &=\pm \gamma _{0}\left[1+4 \cos \left(\displaystyle\frac{\sqrt{3} b p_{z}}{2\hbar }\right)\cos \left(\displaystyle\frac{\pi s}{m}\right)\right. \left.+4\cos ^{2}\left(\displaystyle\frac{\sqrt{3} b p_{z}}{2\hbar }\right)\right]^{1/2}, \end{eqnarray} \end{document}Eq. 23[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} R_{cv}(p_{z},s) &=- \displaystyle\frac{\sqrt{3}b\gamma _{0}^{2}}{2\mathcal {E} _{c}^{2}(p_{z},s)}\sin \left( \frac{\sqrt{3} b p_{z}}{2\hbar }\right)\sin \left(\frac{\pi s}{m}\right)\,, \end{eqnarray} \end{document}Eq. 24[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} R_{cn} & =\displaystyle \frac{3 b m}{2\pi }, \quad a = \frac{2\pi \hbar }{\sqrt{3} b}, \end{eqnarray} \end{document}Finally, let us obtain a simplified expression for the low-frequency conductivity of metallic SWNTs. Before doing so, recall that zigzag (m, 0) SWNTs are metals when index m is a multiple of 3, while armchair (m, m) SWNTs are always metals. When the frequency of the external electromagnetic field is below the frequency of the interband electron transitions, the intraband motions of the electrons give a dominant contribution to the conductivity of metallic SWNTs. This means that the low-frequency conductivity of a metallic SWNT is defined by Eq. 14 with great accuracy. Equation 14 can be further simplified for SWNTs of not very big radii (m < 50) as the main contribution to the integral is due to sub-bands s crossing the Fermi level. The Fermi surface in SWNTs is defined by the set of points satisfying the condition [TeX:] \documentclass[12pt]{minimal}\begin{document}$\mathcal {E}_{c,v}(p_F,s) = 0$\end{document}. In the vicinity of the Fermi level the dispersion law of electrons in metallic SWNTs has the following approximated form:1 Eq. 25[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{equation} \mathcal {E}_{c,v}(p_z,s) \approx \pm v_F |p_z - p_F|, \end{equation} \end{document}Eq. 26[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{eqnarray} \int \limits _{p_F - \Delta p_F}^{p_F + \Delta p_F} \frac{\partial \mathcal {E}_c}{\partial p_z}\frac{\partial \rho ^{eq}}{\partial p_z} \, dp_z &=& 2 \displaystyle\int \limits _{p_F}^{p_F + \Delta p_F} \left(\frac{\partial \mathcal {E}_c}{\partial p_z}\right)^2\frac{\partial \rho ^{eq}}{\partial \mathcal {E}_c} dp_z\nonumber\\ &\approx& 2 v_F \int \limits _{0}^{\mathcal {E}_c(p_F + \Delta p_F,s)} \frac{\partial \rho ^{eq}}{\partial \mathcal {E}_c} d\mathcal {E}_c \nonumber \\ &=& 2 v_F \lbrace \rho ^{eq}[\mathcal {E}_c(p_F + \Delta p_F,s)]-\rho ^{eq}(0)\rbrace\nonumber \\ &=& -2 v_F, \end{eqnarray} \end{document}In zigzag SWNT sub-bands s = m/3 and s = 2m/3 crosses the Fermi level ones. In armchair SWNTs the sub-band s = m crosses the Fermi level twice. This means that the integral in Eq. 14 is approximately equal to −4vF both for metallic zigzag and armchair SWNTs. Thus, the following approximated expression for the conductivity of metallic SWNTs can be obtained: Eq. 27[TeX:] \documentclass[12pt]{minimal}\begin{document} \begin{equation} \sigma = i\, \frac{3 b\gamma _0 e^2 }{\pi ^2 R_{cn}\ \hbar ^2(\omega +i\tau _1)}, \end{equation} \end{document}Conductivity spectra of semiconducting (14,0) SWNT and metallic (15,0) SWNT are presented in Fig. 1. As one can see, in the low-frequency region the values of the conductivity of (15,0) SWNT calculated using approximated Eq. 27 are in good agreement with the conductivity values obtained by Eq. 13. However, in the high-frequency region contribution of the interband electron transitions becomes dominant and approximation 27 is no more applicable. In contrast to metallic SWNTs, the conductivity band of semiconducting SWNTs is practically unoccupied at room temperature. This means that the contribution of the intraband electron motions to the conductivity of semiconducting SWNTs is always small and thus the contribution of the interband electron transitions given by Eq. 15 always needs to be accounted for. Note that surface conductivity unit Ω−1 differs from the volume conductivity unit Ω−1cm−1. 4.Concluding RemarksIn this tutorial the method of the SWNT surface conductivity calculation is discussed. Equations of motions for the density matrix of the π-electron subsystem in the SWNT illuminated by the plane monochromatic electromagnetic wave were solved analytically by the perturbation method and the expressions for the linear conductivity of achiral SWNTs were obtained. All the parameters and functions necessary to calculate the SWNT conductivity without referring to any other sources are indicated. Both SI and Gaussian units can be used. AcknowledgmentsThis research was partially supported by the Belarus Republican Foundation for Fundamental Research under Project Nos. F10CO-020 and N. EU FP7 under Project No. FP7-266529 BY-NanoERA. A.M. is grateful to Dr. Sergey Maksimenko, Dr. Gregory Slepyan, and Professor Akhlesh Lakhtakia for their invaluable help in developing the methods presented in the tutorial. ReferencesJ.-C. Charlier, X. Blase, and S. Roche,
“Electronic and transport properties of nanotubes,”
Rev. Mod. Phys., 79 677
–732
(2007). http://dx.doi.org/10.1103/RevModPhys.79.677 Google Scholar
Ph. Avouris, M. Freitag, and V. Perebeinos,
“Carbon-nanotube photonics and optoelectronics,”
Nat. Photon., 2 341
–350
(2008). http://dx.doi.org/10.1038/nphoton.2008.94 Google Scholar
G. Hanson,
“Fundamental transmitting properties of carbon nanotube antennas,”
IEEE Trans. Antennas Prop., 53 3426
–3435
(2005). http://dx.doi.org/10.1109/TAP.2005.858865 Google Scholar
G. Ya. Slepyan, M. V. Shuba, S. A. Maksimenko, and A. Lakhtakia,
“Theory of optical scattering by achiral carbon nanotubes and their potential as optical nanoantennas,”
Phys. Rev. B, 73 195416
(2006). http://dx.doi.org/10.1103/PhysRevB.73.195416 Google Scholar
C. Rutherglen and P. Burke,
“Nanoelectromagnetics: Circuit and electromagnetic properties of carbon nanotubes,”
Small, 5
(8), 884
–906
(2009). http://dx.doi.org/10.1002/smll.200800527 Google Scholar
G. Ya. Slepyan, M. V. Shuba, S. A. Maksimenko, C. Thomsen, and A. Lakhtakia,
“Terahertz conductivity peak in composite materials containing carbon nanotubes: Theory and interpretation of experiment,”
Phys. Rev. B, 81 205423
(2010). http://dx.doi.org/10.1103/PhysRevB.81.205423 Google Scholar
A. M. Nemilentsau, M. V. Shuba, G. Ya. Slepyan, P. P. Kuzhir, S. A. Maksimenko, P. N. D’yachkov, and A. Lakhtakia,
“Substitutional doping of carbon nanotubes to control their electromagnetic characteristics,”
Phys. Rev. B, 82 235424
(2010). http://dx.doi.org/10.1103/PhysRevB.82.235424 Google Scholar
A. M. Nemilentsau, G. Y. Slepyan, S. A. Maksimenko, A. Lakhtakia, and S. V. Rotkin,
“Scattering of the near field of an electric dipole by a single-wall carbon nanotube,”
J. Nanophoton., 4 041685
(2010). http://dx.doi.org/10.1117/1.3416909 Google Scholar
A. M. Nemilentsau, G. Ya. Slepyan, S. A. Maksimenko, A. Lakhtakia, and S. V. Rotkin, Phys. Rev. B, 82 235411
(2010). http://dx.doi.org/10.1103/PhysRevB.82.235411 Google Scholar
G. Ya. Slepyan, S. A. Maksimenko, A. Lakhtakia, O. Yevtushenko, and A. V. Gusakov,
“Electrodynamics of carbon nanotubes: Dynamic conductivity, impedance boundary conditions, and surface wave propagation,”
Phys. Rev. B, 60 17136
–17149
(1999). http://dx.doi.org/10.1103/PhysRevB.60.17136 Google Scholar
G. Ya. Slepyan, A. A. Khrutchinskii, A. M. Nemilentsau, S. A. Maksimenko, and J. Herrmann,
“High-order optical harmonic generation on carbon nanotubes: Quantum-mechanical approach,”
Int. J. Nanosci., 3
(3), 343
–354
(2004). http://dx.doi.org/10.1142/S0219581X04002152 Google Scholar
A. M. Nemilentsau, G. Ya. Slepyan, A. A. Khrutchinskii, and S. A. Maksimenko,
“Third-order optical nonlinearity in single-wall carbon nanotubes,”
Carbon, 44
(11), 2246
–2253
(2006). http://dx.doi.org/10.1016/j.carbon.2006.02.035 Google Scholar
A. M. Nemilentsau, G. Ya. Slepyan, and S. A. Maksimenko,
“Rabi oscillations and saturable absorption effect in single-wall carbon nanotubes,”
J. Phys. Conf. Ser., 248
(1), 012015
(2010). http://dx.doi.org/10.1088/1742-6596/248/1/012015 Google Scholar
J. Maultzsch, R. Pomraenke, S. Reich, E. Chang, D. Prezzi, A. Ruini, E. Molinari, M. S. Strano, C. Thomsen, and C. Lienau,
“Exciton binding energies in carbon nanotubes from two-photon photoluminescence,”
Phys. Rev. B, 72 241402
(2005). http://dx.doi.org/10.1103/PhysRevB.72.241402 Google Scholar
|