1.

Introduction

Electromagnetic scattering from nanometer-scale objects has long been a topic of large interest and relevance to fields from astrophysics or meteorology to biophysics, medicine, and material science.^{1, 2, 3, 4} In the last few years, small particles with resonant magnetic properties are being explored as constitutive elements of new metamaterials and devices. Magnetic effects, however, cannot be easily exploited in the visible or infrared regions due to intrinsic natural limitations of optical materials and the quest for magnetic plasmons and magnetic resonant structures at optical frequencies^{5, 6, 7} has then been mainly focused on metallic structures. The unavoidable problems of losses and saturation effects inherent to these metamaterials in the optical and near-infrared regimes have stimulated the study of high-permittivity particles as their constitutive elements:^{8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18} For very large permittivities, small spherical particles present well defined sharp resonances;¹ either electric or magnetic resonant responses can then be tuned by choosing the appropriate sphere radius. However, the applicability of conventional homogenization procedures to determine the constitutive parameters of composites of resonant spheres cannot be implemented without due regard to their limitations on volume fraction and size parameter.¹⁹

In the presence of both electric and magnetic properties, the scattering characteristics of a small object present marked differences with respect to pure electric or magnetic responses. Even in the simplest case of small or dipolar scatterers, remarkable scattering effects of magnetodielectric particles were theoretically established by Kerker²⁰ concerning suppression or minimization of either forward or backward scattering. Intriguing applications in scattering cancellation and cloaking^{21, 22, 23} and magneto-optical systems,^{24, 25, 26, 27} together with the unusual properties of the optical forces on magnetodielectric particles,^{28, 29} have renewed interest in the field.

The striking characteristics of the scattering diagram of small (Rayleigh) magnetodielectric particles^{20, 30, 31} were obtained assuming arbitrary values of relative permittivity and permeability.

Nevertheless, no concrete example of such particles that might present those interesting properties in the visible or infrared regions had been proposed. Very recently, it has been shown^{32, 33} that submicrometer silicon spheres present dipolar magnetic and electric responses, characterized by their respective first-order Mie coefficient, in the near-infrared, in such a way that either of them can be selected by choosing the illumination wavelength. In a later work, it has also been shown^{29, 34} that Si spheres constitute such a previously quested real example of a dipolar particle with either electric and/or magnetic response, of consequences both for their emitted intensity and behavior under electromagnetic forces.

These properties should not be restricted to Si particles, but should also apply to other dielectric materials with relatively moderate refraction index. In the present work, we discuss the effects associated to the interference between electric and magnetic dipoles in germanium spheres. The paper is structured as follows. Based on the exact Mie theory, in Sec. 2 we show that both the extinction cross section and the scattering diagrams of submicrometer Ge spheres in the infrared region can be well described by dipolar electric and magnetic fields, being quadrupolar and higher order contributions negligible in this frequency range. Specifically, the scattering diagrams calculated at the generalized Kerker's (GK) conditions are shown to be equivalent to those previously reported^{20, 31} for hypothetical magnetodielectric particles. Following previous work regarding the peculiar properties of optical forces at GK conditions,²⁹ in Sec. 3 we analyze the consequences of the strong scattering anisotropy on the radiation pressure on Ge particles.

2.

Extinction Cross Sections and Scattering Anisotropy of Submicrometer Germanium Spheres

Consider a nonabsorbing dielectric sphere of radius a and permittivity [TeX:] \documentclass[12pt]{minimal}\begin{document}$\epsilon _p=m_p^2$\end{document} ${\epsilon }_p=m_p^2$ in an otherwise uniform medium with real relative permittivity ε and refractive index [TeX:] \documentclass[12pt]{minimal}\begin{document}$m=\sqrt{\epsilon \mu }$\end{document} $m=\sqrt{\epsilon \mu }$ . The relative permeability μ_p of the sphere and of the surrounding medium, μ, are both assumed to be μ_p = μ = 1 (even though in some of the equations to be written in this paper, μ will explicitly be included for the sake of comprehensiveness of the theory) .

Under plane wave illumination, and assuming linearly polarized light, the incident wave is described by

In the small particle limit (x ≡ ka ≪ 1) and large particle permittivities (m_p/m ≫ 1) the extinction cross section presents characteristic sharp resonance peaks. At each resonance, the extinction cross section is of the order of λ² and it is independent of the particle size or refractive index.¹ Interesting applications of well defined Mie resonances, associated to low loss and large dielectric constants, are accessible for different materials at microwave and terahertz frequencies. However, as m_p decreases there is an increasing overlap between the cross section peaks, and the resonant character weakens until it disappears. Since usually nonabsorbing materials present low refractive index in the near-infrared and visible frequency ranges, Mie resonances of small particles in these regimes have not been considered in detail. However, a recent analysis of the cross section of submicrometer dielectric particles³³ show that well defined resonances can be found for materials with relative refractive index as low as m_p ∼ 3m.

Germanium submicrometer particles are a good candidate to explore the effects associated to the interference between electric and magnetic responses. In the micrometer wavelength regime, within the transparent region of germanium (λ ≳ 1.4 μm), the refraction index can be well approximated by a real constant [TeX:] \documentclass[12pt]{minimal}\begin{document}$m_p \approx \sqrt{16} = 4$\end{document} $m_p\approx \sqrt{16}=4$ (see, for example, Ref. 35). The calculated exact extinction (or scattering) cross section of a 240 nm radius Ge sphere in vacuum (m = 1) is plotted in Fig. 1. Although there is an overlap between the first dipolar peaks, the first dipolar magnetic resonance (at λ ≈ 2000 nm) and the electric dipolar resonance (at λ ≈ 1500 nm) are still very well defined. As we will see, this overlap plays a key role in determining the peculiar scattering diagrams of Ge particles. Interestingly, for wavelengths larger than λ ≈ 1400 nm, the cross section is completely determined by the first b₁ and a₁ coefficients. Therefore, Eq. 4 becomes

Fig. 1

Extinction cross section Q_ext versus the wavelength λ for a 240 nm Ge sphere (the refraction index m_p = 4 is constant and real in this wavelength range). The contribution of each term in the Mie expansion is also shown. The red line corresponds to the magnetic dipole contribution.

Dipolar particles are usually characterized by their electric and/or magnetic complex polarizabilities, α_e and α_m, which may be written in the form^{28, 33}

For a pure electric or a pure magnetic dipole, in the absence of interferences, the far field radiation pattern is symmetrically distributed between forward and backward scattering. However, when we consider the coherent contribution of both electric and magnetic dipoles, the radiation pattern is mainly distributed in the forward or backward region according to whether [TeX:] \documentclass[12pt]{minimal}\begin{document}$\Re (\alpha _{e} \alpha _{m}^{*})$\end{document} $\Re \left({\alpha }_e{\alpha }_m^{*}\right)$ is positive or negative, respectively.^{28, 29} Interestingly, at the GK conditions |ε⁻¹α_e|² = |μα_m|², the scattered intensity should be independent of the incident polarization angle:

i) The intensity in the backscattering direction can be exactly zero whenever a₁ = b₁ or

ii) Although the intensity cannot be exactly zero in the forward direction (causality imposes ℑ{α_e}, ℑ{α_m} > 0), in absence of particle absorption, the forward intensity presents a minimum at²⁹

Figure 2 shows the real and imaginary parts of the polarizabilities [Eq. 8] for a Ge sphere with a = 240 nm. One sees the values of λ at which ℑ{α_e} = ℑ{α_m}, which are where the first and second GK conditions hold for these polarizabilities.

Fig. 2

Normalized real and imaginary parts of both the electric and magnetic polarizabilities for a Ge sphere of radius a = 240 nm; ε_p = 16 and μ_p = 1. The host medium has ε = μ = 1. The first and second GK conditions (at λ = 2193 and λ = 1823 nm, respectively) are marked by the right and left vertical lines, respectively.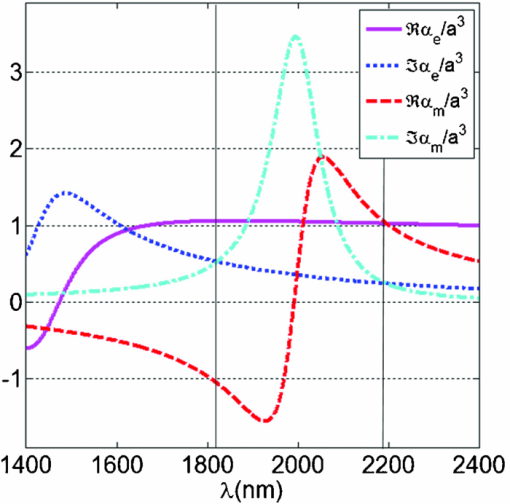

In order to check the validity of the dipolar approach and confirm the predictions at the GK conditions, we have computed the exact scattering diagram from the full Mie expansion. The numerical results are shown in Fig. 3. While the backward intensity drops to zero at the first GK condition wavelength, at the second condition, although the most of the intensity goes backward, the scattering diagram presents a very small peak in the forward direction. As expected from the extinction cross section, the far field pattern is fully consistent with the dipolar approximation. In particular, at the GK conditions it is independent of the incoming polarization. Dielectric spheres and, in particular, lossless Ge particles in the near-infrared, then constitute a realizable laboratory to observe such interesting scattering effects.

Fig. 3

Scattering diagrams for the 240 nm Ge nanoparticle of Fig. 1. Both polarizations, with the incident electric field parallel (TM or P polarization) or normal (TE or S polarization) to the scattering plane are considered.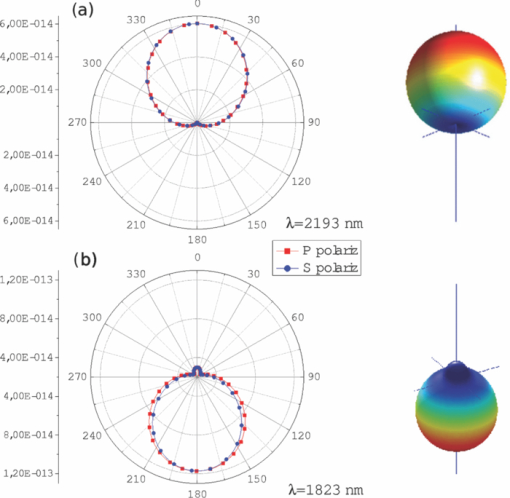

3.

Effects on Optical Forces

Let us now discuss some of the consequences of the GK condition on optical forces. The theory of the force on a dipolar magnetic particle has recently been developed.^{28, 36} This includes pure dielectric particles which can be well described by its first two electric and magnetic Mie coefficients.²⁸ The time averaged force on a dipolar particle can be written as the sum of three terms:²⁸

At the first GK condition, Eq. 11, the interference term of Eq. 13 cancels out the magnetic contribution and we obtain 〈F〉 = 〈F_e〉. At the second GK condition, Eq. 12, where the backscattering is enhanced, 〈F〉 = 3〈F_e〉. Notice that at both GK conditions the scattering cross section is exactly the same; however, the radiation pressures differ by a factor of 3. These properties are illustrated in Fig. 4, where we show the different contributions to the total time averaged force on a submicrometer Ge particle.

Fig. 4

Different contributions to the total radiation pressure versus the wavelength, for the Ge particle of Fig. 1. Normalization is done by F₀ = kεa³|E₀|²/2. Again, the vertical lines mark the first and second GK conditions. Notice that when the first GK condition is fullfilled, i.e., ℑα_e = ℑα_m and ℜα_e = ℜα_m, 〈F〉 = 〈F_e〉 = 〈F_m〉 = −〈F − m〉.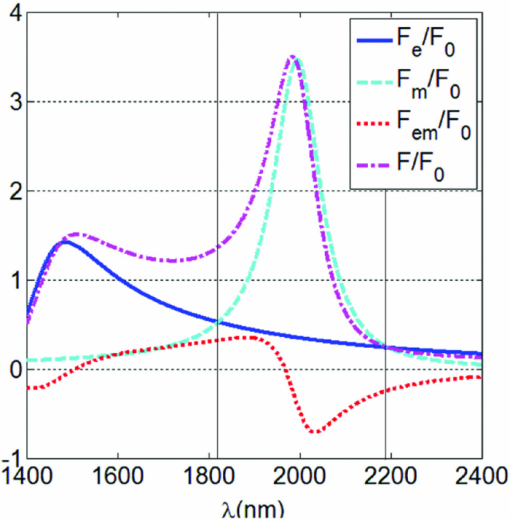

The strong peak in the radiation pressure force is mainly dominated by the first “magnetic” Mie resonance. This is striking and in contrast with all previous beliefs about optical forces on dipolar dielectric particles, that assumed that these forces would solely be described by the electric polarizability. It is also common to assume that for dielectric particles the real part of the polarizability is much larger than its imaginary part. As a matter of fact, this is behind the development of optical tweezers, in which gradient forces (that are proportional to ℜ{α_e}), dominate over the radiation pressure or scattering force contribution (which is proportional to ℑ{α_e}).³⁷ However, as the size of the particle increases, and for any dielectric particle, there is a crossover from electric to magnetic response as we approach the first Mie resonance, the point at which the response is absolutely dominated by the magnetic dipole. Moreover, just at the resonance, and in absence of absorption, ℜ{α_m} = 0 and ℑ{α_m} = 3/(μ2k³). Then, the radiation pressure contribution of the magnetic term dominates the total force 〈F〉 ≃ 〈F_m〉 ≈ (ε|E₀|²/2)[3/(2k²)]. Namely, in resonance the radiation pressure force presents a strong peak, the maximum force being independent of both material parameters and particle radius.

4.

Conclusions

In summary, we have predicted that real small dielectric particles made of nonmagnetic materials present interesting scattering properties similar to those previously reported for somewhat hypothetical magnetodielectric particles,²⁰ resulting from an interplay between real and imaginary parts of both electric and magnetic polarizabilities. The exact scattering diagram, computed from the full Mie expansion, of submicrometer Ge particles in the infrared, was shown to be consistent with the expected result for dipolar electric and magnetic scattering. Then we showed that these unusual scattering effects also affect the radiation pressure on these small particles; specifically, the generalized Kerker's conditions have been tested on Ge spheres. Submicro-meter Ge particles constitute an excellent laboratory to observe such new scattering phenomena and force effects. Being Ge permittivitys is higher than Si, the present work extends the range of some possible applications (previously suggested for silicon particles), to systems where the host medium presents refractive index larger than vacuum.

The extraordinary scattering properties discussed here will strongly affect the dynamics of particle confinement in optical traps and vortex lattices³⁸ governed by both gradient and curl forces.^{28, 39} The interference between electric and magnetic dipoles suggest also intriguing possibilities regarding resonant coupling between the scattered dipolar field and guided modes in confined geometries.⁴⁰ We do believe that our results will stimulate further experimental and theoretical work in different directions, from optical trapping and particle manipulation to cloaking and the design of optical metamaterials based on lossless dielectric particles.