|
|
1.IntroductionThe electron gas undergoes, in some conditions, a phase transition to bound pairs of electrons (the so-called Cooper pairs), which replace electrons as the fundamental agent of the electronic properties. Cooper pairs are, from the point of view of their electric charge, objects qualitatively identical to the underlying electrons. From the point of view of their spin, on the other hand, they become integer-spin particles, that is, from the spin-statistics theorem, bosons rather than fermions. This shift of statistical paradigm of the carriers—from Fermi to Bose-statistics—results in the outstanding behavior of superconductivity, that is, conduction of electric charge by a macroscopic coherent wavefunction (akin to a Bose–Einstein condensate). It has taken some time to capture the fundamental and universal features of this phenomenon and set them apart from particularities of certain cases only. The gap of excitations, responsible for zero resistivity, for instance, results from the long-range nature of the Coulomb interaction, but gapless superconductivity is also possible. One of the central, fundamental concepts of superconductivity is that of a coherent quantum state of charged bosons. Although superconductivity was discovered empirically, and its theoretical construction consisted in assembling a puzzle, it is now possible to envisage engineering superconducting phases in other systems, based on this understanding of condensation of charged bosons. If superconducting phases can be identified in other systems, progresses will be quick for the understanding of cuprate superconductivity, which still eludes compelling theoretical explanation of its intrinsic mechanism. A system that is making rapid and impressive progress in terms of creating and controlling macroscopic quantum states is that of microcavity exciton-polaritons1 (see Ref. 2 for a review). These quasi-particles which combine properties of light (cavity photons) and matter (quantum well excitons) have been noted for their predisposition to accumulate in macroscopic number in a single or few quantum states.3,4 They have many advantages from a practical point of view, such as their 2D geometry, which allows straightforward manipulation by lasers impinging at an angle, and their short lifetime, which allows continuous monitoring of the system, reconstructing its internal dynamics also by angle-resolved spectroscopy.5 The pumping can be either coherent (driving states in parametric scattering configurations)6–10 or incoherent (with a constant flow of unrelated particles relaxing into the ground state).11–16 In nitride systems, the formidable claim has been made of room-temperature Bose–Einstein condensation.17,18 Recently, there has been great interest in propagation of polariton fluids19,20 and their superfluid properties,21 with reports of quantized vorticity22,23 and persistent currents.24 These rising stars of macrosopic coherence have also been proposed to realize another much sought after quantum phase at high-temperature: superconductivity. Polariton condensates cannot conduct electric current themselves, being neutral particles. One of the proposed implementations involves “ quatrons” (or quadrions) rather than polaritons.25 Quatrons are bound states of two electrons with a polariton. They remain bosons from spin-addition rules but carry an electric charge. A Bose condensate of quatrons would, through its superfluid propagation, exhibit superconductivity. To date, however, the existence of the quatron, predicted theoretically,25 has not been found experimentally. Recently, we have approached the problem from another, and more conventional, angle, that of the Bardeen, Cooper, and Schrieffer (BCS) mechanism26 with an important new feature: replacement of phonons by Bose-condensed exciton-polaritons in the role of a binding agent between electrons. In the present paper, we generalize the model proposed in Ref. 26 to describe a wide range of hybrid Bose–Fermi semiconductor systems where a Bose–Einstein condensate of neutral quasi-particles (excitons or exciton-polaritons) coexists with a Fermi sea of electrons. We show that indeed such systems are promising for observation of (high-temperature) superconductivity. Moreover, as the superconducting gap and critical temperature are very sensitive to the concentration of bosons in the system and the latter may be controlled by direct optical excitation, light-induced superconductivity in semiconductor heterostructures appears to be possible. In this work we closely follow the BCS approach, generalized and adapted to the case of superconductivity mediated by a Bose–Einstein condensate. Solving the gap equation in this case turns out to be a nontrivial problem, requiring careful analysis. 1.1.BCS with a Bose–Einstein Condensate as a Binding AgentBCS is a pillar of superconductivity theory, which relies on three main tenets:
These are the three insights that were mainly contributed by Cooper, Bardeen, and Schrieffer, respectively, and that they could assemble into the BCS theoretical edifice and exploit to reproduce strikingly or predict successfully most of the superconductivity phenomenology. The first point follows from Cooper’s observation27 that an arbitrarily small attractive interaction between two electrons on top of the Fermi sea leads to a bound state (the Cooper pair), thanks to the truncation of the momentum space for states with wavevector (Fermi wavevector). This is a general result, which follows from the Bethe-Goldstone equation for the two-electron problem. The second point is the identification of an effective attraction between electrons that normally experience bare Coulomb repulsion. This attraction is attributed for conventional superconductors to an interaction through phonons, the Bardeen-Pines potential,28 that consists, vividly, of one electron wobbling the lattice at a first time, which affects another electron at a second time (and at a larger timescale, since the lattice dynamics is much slower than that of electrons).29 If the frequency of the lattice vibration is smaller than that of the propagating electron, the net effect results in an effective attraction [Leggett offers an insightful toy model of coupled oscillators to capture the essence of the interaction character (attractive or repulsive)].30 The last point is the so-called BCS state, which is a coherent superposition of paired bound states and which brings the two-particle Cooper effect to a collective behavior of all electrons in the system.31 With these three ingredients put together, the BCS theory is complete.32 For our purposes, points 1 and 3 will be regarded as fundamental and well-established features of (BCS type of) superconductivity. Point 2, which might appear a mere desiderata for point 1 to apply, leaves us room for identifying and designing new types of attractive potentials, optimizing the range of applicability and strength so as to obtain robust superconductivity (e.g., holding at high temperatures or high magnetic fields) or its manifestation in a new class of systems (in microcavities). Bardeen himself, with coworkers,33 investigated possibilities to engineer a more robust BCS state in a bilayer structure where excitons replace phonons as mediators of the interaction. The idea of substituting phonons by excitons was pioneered by Little34 and developed by Ginzburg,35 who coined the term and theorized the possibility of high-temperature superconductivity, much before it came to fruition with cuprates.36 Cuprates, however, exploit another (still unknown) mechanism different to BCS.37 In the following, we revisit the Ginzburg mechanism, based on BCS, with emphasis on maximizing the strength of interaction between electrons, so as to maintain their binding, and therefore superconductivity, to higher temperatures. The text is organized as follows: in Sec. 2, we give a short overview of the BCS mechanism and the exciton (Ginzburg) mechanism, outlining the points of special interest in our case. In particular, we introduce the gap equation. In Sec. 3, we introduce our hybrid Bose–Fermi system configuration, its Hamiltonian and microscopic interactions, and the effective electron-electron Hamiltonian that results from a mean-field approximation for the condensate and the usual Frölich transformation. We obtain the shape of the effective electron-electron interaction , that we find to be quite different in character to the Cooper (square well) potential. We also consider possible variations of our scheme, namely, a microcavity with a condensate of exciton-polaritons and a condensate of indirect excitons in coupled quantum wells.38 The system of coupled quantum wells explored by several groups39,40 might be easier to realize and study (it does not need a cavity) and presents some interesting differences as compared to the polariton system. On the other hand, polaritons condense at much higher temperatures.18 In Sec. 3.2, we study the gap equation for a Bose condensate-mediated effective interaction. Because the potential is not positive-definite, the problem is not well-posed numerically. We propose a simplified potential and an approximate solution of the gap equation, which we motivate by studying its validity on well-established approximations. We obtain the critical temperature in this case. In Sec. 4, we give our conclusions and perspective on this new application of excitons and polaritons and discuss how to measure the effect experimentally. 2.BCS and Ginzburg MechanismsSuperconductivity is a fundamental property of solids. At low enough temperatures, most metals superconduct. As the mechanism is rooted in quantum mechanics, temperatures are expected to be very low and indeed this is the case for all metals. After considerable theoretical efforts from various groups, a compelling theoretical model was assembled by Bardeen, Cooper, and Schrieffer, the so-called BCS theory.29 The model provides the critical temperature: where, in conventional superconductivity, is the Debye energy, and with the density of electrons at the Fermi energy and the electron-phonon coupling strength. The Debye energy is, in good approximation, the maximum energy that can be carried by a phonon. The mechanism therefore relies heavily on phonons, as was realized empirically before the advent of BCS (good conductors, for instance, are bad superconductors, since is small; also through the isotope effect, which correlates critical temperature with mass of the crystal atoms, and thus with resonance frequency). The exponential form and the presence of show that the effect is a collective one involving all electrons, which have formed a new phase of matter that cannot be approached perturbatively by the independent electron pictures (since has no Taylor expansion around zero). Based on the theory, and accumulated experience, it was widely accepted that critical temperatures would not exceed a few tens of Kelvins, since the Debye energy, which can be quite large in some systems (hundreds of Kelvins), is exponentially reduced. In all conventional superconductors (the so-called weak-coupling regime).Ginzburg made the obvious but daring assumption that to achieve higher critical temperatures—crucial for technical applications which can easily be understood to be momentous—it is enough to find a system where and/or are increased. Replacing phonons by excitons, for instance, Ginzburg found that values , as well as , are obtained, yielding temperatures of several hundred Kelvin.41 High critical temperatures have been later reported in cuprates36 and nowadays, temperatures as high as 125 K are obtained in systems such as Tl-Ba-Cu-oxide. Cuprate superconductivity does not appear to follow the BCS pattern.42 On the other hand, all attempts to date to realize the exciton mechanism or a variation of it have remained fruitless. This is this mechanism, rooted in BCS, which we consider in this text. Since it consists in substituting the phonons of conventional BCS—or the excitons of Ginzburg scheme—by a Bose–Einstein condensate (BEC) of excitons or exciton-polaritons, the starting point for its microscopic description starts with the same zero temperature gap equation: where is the effective interaction between electrons with wavevectors and and energy . The gap can be identified as the macroscopic wavefunction of a Cooper pair, which is also the order parameter for the superconducting phase. If it is nonzero, the system is in the superconducting state. A realistic microscopic treatment of is very complicated. A simplified version is provided by the Jellium model, which is a toy model of a metal that gives predominance to electron-electron interactions, that is, in particular, the underlying crystal is approximated as a uniform (structureless) background (like a “jelly”) in which the interacting electron gas evolves under its own self-interactions and the overall charge cancellation of the background. A popular effective interaction is given by the Bardeen-Pines potential30 which is derived from the microscopic form of the electron-lattice interaction: with q the phonon wavevector. In Eq. (3a), is the Thomas-Fermi screening parameter and is the phonon dispersion. The first term between the brackets is bare Coulomb repulsion, and the second term, which is frequency dependent, follows from the perturbative coupling to the lattice, tracing out the phonons.The physical meaning of Eq. (3a) is at the heart of the phonon-mediated mechanism. The interaction is dependent, which means, in Fourier transform, time dependent. This reflects the famous retardation effect in superconductivity. This effect is based on the strong difference between the electron Fermi velocity in metals and the sound velocity. Roughly speaking, a fast electron from the Fermi surface creates a slow phonon and goes away. After some time, another fast electron arrives and absorbs the slow phonon. The average distance between these two electrons remains of the order of 100 nm, the distance at which the screened Coulomb repulsion can be safely neglected. Due to the retardation effect, a weak phonon-mediated attraction of electrons wins over their Coulomb repulsion and provides formation of Cooper pairs at low enough temperatures. 3.Interaction HamiltonianA sketch of the structure we propose appears in Fig. 1(c). A QW is doped negatively (with density of electrons ) and is put in contact with another QW where excitons are formed and are stable. The first (lower) QW hosts the 2DEG which is to undergo superconductivity while the second (upper) QW hosts the condensate of excitons that is to mediate it. This structure can also be placed at the maximum of the optical field confined in a microcavity26 (formed by two Bragg mirrors facing each other). The latter configuration also has the advantage that two excitonic- QWs can sandwich the 2DEG-QW since in this case the condensate is delocalised in the entire structure thanks to the photon fraction of the polariton. This allows an increase by a factor of 2, or more if the multilayer structure is further repeated, of the densities achievable in this system. The drawback of microcavities is a short radiative lifetime of polaritons. In order to maintain the polariton condensate one needs to pump it resonantly by a high-intensity laser, which may lead to undesirable heating of the system. The alternative system which we consider is a condensate of long-living spatially indirect excitons in coupled QWs, separated by a thin but high barrier from a QW containing a two-dimensional electron gas (2DEG). This system is simpler to realize as it does not contain the optical cavity. The condensate of indirect excitons may be maintained by a low-intensity optical excitation. Moreover, indirect excitons in coupled QWs possess very significant dipole moments which strengthens their interaction with electrons from a 2DEG. However, Bose condensates of indirect excitons have been found only at temperatures below 1 K,38 while condensates of exciton-polaritons are now routinely produced at room-temperature.43 In the following, we compare the advantages of the two respective schemes. Most of the underlying model applies to both equally. We focus more particularly on the microcavity system since it is more general. The exciton system is recovered by decoupling the photons. Fig. 1One of the possible designs to evidence exciton-polariton mediated superconductivity. (a) Polariton (thick blue solid line) and exciton (magenta dashed line) dispersions with schematic representation of scattering of the boson that mediates the interaction between electrons. Also shown in thin blue solid line is the renormalised dispersion , essentially identical to . (b) Corresponding scattering of two electrons on the surface of the Fermi sea, exchanging momentum through scattering of a boson in panel (a). (c) detail of the sandwich structure, showing the doped well (below) containing free electrons and the well hosting the condensate (above) of excitons or of exciton-polaritons. This layer can be sandwiched in different ways. 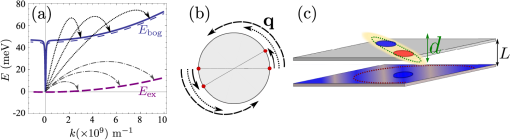 In Fig. 1(a), the exciton (resp. polariton) dispersion is shown in dashed magenta (resp. solid blue). The difference between the bare polariton dispersion (thick blue) and the bogolon dispersion (thin blue) is very small over the range of exchanged momenta of interest (of the order of the Fermi wavevector). The condensate in both cases is at . Scattered particles at any wavevector between and mediate electron-electron interactions on the Fermi sea, as sketched on Fig. 1(b). The model microscopic Hamiltonian is taken as:26 with and the polariton and 2DEG dispersions for the in-plane wavevector , respectively. In the exciton case (without the microcavity), it suffices to replace with in the above. is the electron-polariton interaction, the polariton-polariton interaction and the electron-electron repulsion. We now consider these terms in turn. Parameters assumed are listed in Table 1.Table 1Parameters used in the numerical simulations. In square brackets, the value for the exciton case when the parameter differs from the polariton case, otherwise parameters have been taken the same for comparison.
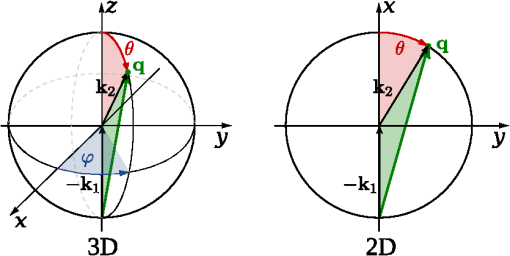
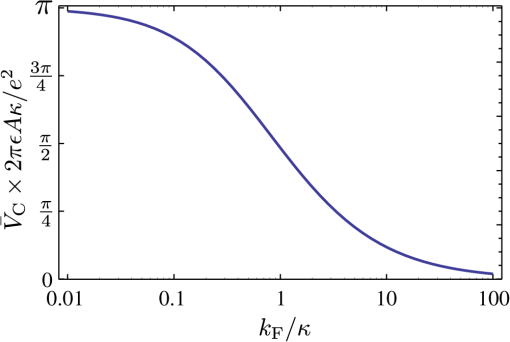
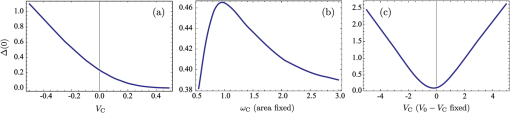
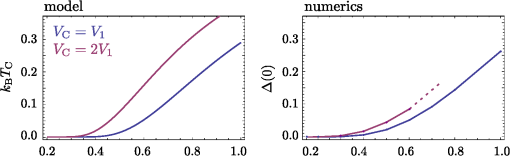
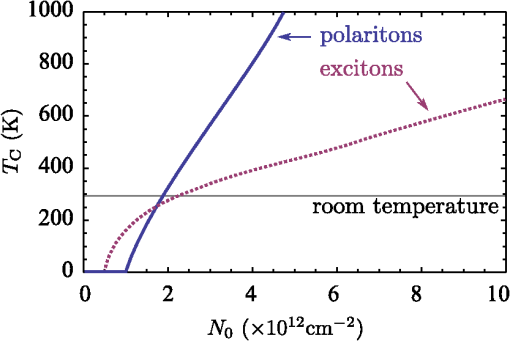
3.1.Electron-Electron InteractionIn the original BCS mechanism, electron-electron repulsion is either neglected altogether or overcome by the attractive mechanism and not manifested outside of the attractive window. We take it into account here since it is a detrimental factor for binding and most of our concern for experimental realization is to optimize this value. The full form of the potential is given by the Yukawa potential: with screening constant . We get rid of the momentum dependence by averaging the potential over the Fermi surface (FS), where: and are the initial and final states of the electrons scattered with the exciton (polariton) from the condensate. The second electron scatters between states and such that . The characteristic energy is that of a bogolon (an elementary excitation of the condensate). In 3D, the FS where these electrons that scatter lie, is the surface of a sphere, while in 2D, it is a circle (we will speak of surface in both cases). The vector difference is therefore joining the two end-points on the surface. If the potential has spherical symmetry , the average of all two vectors on the FS reduces to that where is pinned at one point of the surface (the south pole in Fig. 2) and runs overs the FS. This average, in the particular choice of Fig. 2, is the usual polar integration with describing the surface as (and in 3D) are varied, with: from Al Kashi’s theorem, so that the average potential reads, in 3D: where is the normalization, i.e., the same integral where is replaced by unity. This gives, in 3D: where we integrate over since this is a natural variable in Eq. (7), and, in 2D:Our system is 2D, in which case, from Eqs. (5) and (11): When , both the numerator and the denominator become pure imaginary so their quotient remains real. When , . This is plotted in Fig. 3. Since we are trying to maximize attraction, that is, minimize repulsion, systems with small screening length and large wavevectors should be favored (but these parameters play critically on other aspects of the mechanism and the optimum is not compulsorily ). 3.2.Electron-Exciton InteractionThe electron-exciton or exciton-polariton interaction is one of the most important ingredients of the mechanism, as it ultimately determines the shape of the effective potential. In the microcavity, an electron (from the 2DEG) interacts with a polariton (from the condensate) through its excitonic component, so this is really the electron-exciton interaction that is to be computed,44 weighted by the Hopfield coefficient (the excitonic fraction) . Let us consider, therefore, the scattering of an electron in one of the parallel QW, separated by a distance from the QW with excitons.45 The matrix element of the direct interaction between excitons and electrons reads: where , , correspond to the 2D coordinates of the 2DEG electron, the exciton electron and the exciton hole respectively. The 2DEG electron is described by a plane wave while the electron/hole in the condensate are assumed to be in the 1s bound state with plane wave center-of-mass motion: where , are in-plane coordinates of the center-of-mass of the exciton and relative coordinate of electron and hole in the exciton, and are normal to the QW plane electron and hole envelope functions, respectively. We also consider the existence of a dipole moment for the exciton, which can be intrinsic to the structure, because of spatial separation of electrons and holes in coupled QWs, or (in the case of microcavities) be induced by an internal piezo-electric field, or result from an externally applied electric field. To account for all these possibilities, one can consider the layers of electrons and holes in the exciton shifted in the -direction with respect to the position of the center-of-mass by a distance . The matrix element of the interaction is then computed to be: where Eq. (15a) is the direct electron-exciton interaction that exists even in the absence of a dipole moment of the exciton, and Eq. (15b) is the dipolar interaction. The direct interaction vanishes at small exchanged momenta, while the dipolar-induced one assumes its maximum value here of . Overall, the dipolar interaction is naturally much larger than the direct one, since the exciton is electrically neutral.* These facts are summarized in Fig. 4.Fig. 4Electron-exciton interaction in the geometry of Fig. 1, decomposed as the direct interaction (dashed magenta) and dipolar interaction (solid blue) when the exciton is induced with a dipole moment . The latter is both much larger and maximum at zero exchanged momentum. 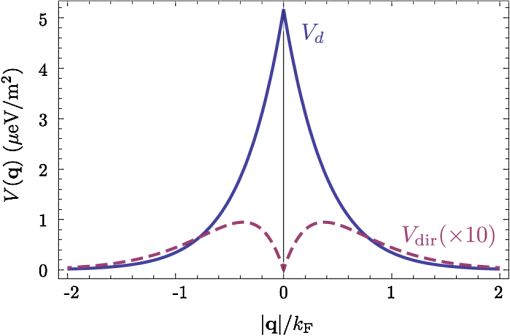 3.3.Polariton-Polariton InteractionWe treat the polariton-polariton interaction within the -wave scattering approximation with strength (where is the exciton Bohr radius, the exciton binding energy and the normalization area. is the exciton Hopfield coeffcient, the square of which quantifies the exciton fraction in the exciton-polariton condensate).46 For interaction between bare excitons, . Exciton-exciton (polariton-polariton) interactions are repulsive, in general. They result in linearization of the elementary excitation spectra, the Bogoliubov dispersion, but its role is not crucial to the mechanism of superconductivity we discuss, since at the wavevectors of interest, the changes brought by this term are very small compared to the kinetic energy of noninteracting excitons (exciton-polaritons). 3.4.Effective InteractionWe now proceed to bring our microscopic model toward a form suited to study Cooper-pairing and superconductivity, that is, we apply the canonical Fröhlich transformation that will result in an effective BCS Hamiltonian. Just as in the case of phonons, we start by getting rid of polaritons. We assume a condensate is formed with mean population . We do not consider which mechanism, coherent or incoherent, is responsible for creating and maintaining this state. We do assume, however, it is coherent and with a definite phase, so that we can apply the mean-field approximation and with the density of polaritons in the condensate. This allows us to obtain the following expression for the Hamiltonian, after diagonalizing the polariton part by means of a Bogoliubov transformation (that leaves the free propagation of electrons and their direct interaction, , invariant): where describes the dispersion of the elementary excitations (bogolons) of the interacting Bose gas, which is very close to a parabolic exciton dispersion at large : where and with the renormalized bogolon-electron interaction strength:The last term of Eq. (16) coincides with the Fröhlich electron-phonon interaction Hamiltonian, which allows us to write an effective Hamiltonian for the bogolon-mediated electron-electron interaction. This results in an effective interaction between electrons, of the type . The effective interaction strength reads , with: Equation (19) recovers the boson-mediated interaction potential obtained for a Bose–Fermi mixture of cold atomic gases,47 in the limit of vanishing exchanged wavevectors. It describes the BEC induced attraction between electrons. Remarkably, it increases linearly with the condensate density . This represents an important advantage of this mechanism of superconductivity with respect to the earlier proposals of exciton-mediated superconductivity,33,34,48 as the strength of Cooper coupling can be directly controlled by optical pumping of the exciton-polariton condensate. The attractive potential is displayed for various exchanged energies in Fig. 5, as a function of , defining the exchanged momentum expressed directly through the angle defined in the Fermi circle (cf. Fig. 2). As commented earlier, the negative part corresponds to attraction, and the potential alternates between repulsive and attractive character, obtained at different exchanged momenta. We do not want to keep track of such complicated wavevector dependence, and therefore will average the interaction over the Fermi sea. A notable feature is, for most values of , the presence of a pole , where . As is seen in the figure, separates the attractive part from the repulsive part. The average will bring the additional convenience of canceling such divergencies. We note as well that the spectrum of excitations of the exciton-BEC may be changed in the presence of the electron gas, so that their eventual dispersion may be different to .49 This has no effect on the Cooper-pairing of electrons which we discuss here. Fig. 5Effective electron-electron interaction as a function of θ, defining the exchanged momentum on the Fermi sea at energies , 50, and 60 meV, respectively. The potential is symmetric around . In the first case, the whole dependency (over ) is shown, with a first zoom in the inset showing two poles and another the attractive region that is of small amplitude but extends over a large range. With increasing energies, the poles recede towards smaller values of with a dominating effect of the repulsive (positive) energy. In the central panel, in dashed magenta, the regularized potential is superimposed. 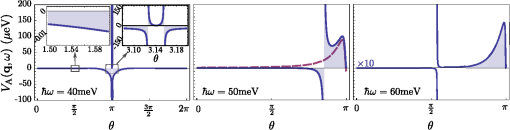 We therefore wish to perform the average where , as seen previously. Since is symmetric around we perform the integral only. The integral would be easily computed numerically if there were no pole. There are dedicated numerical methods to compute principal values numerically,50,51 but in our case, since the pole is first order, it is enough to isolate it analytically by defining so thatwhere and the first integral is regular (it is shown in Fig. 5 in dashed magenta). The integration (average) is then straightforward and produces the results shown in Fig. 6.Fig. 6Exchanged-momentum averaged interaction between electrons of the 2DEG, as is increased. It is dimensionless and is attractive (resp. repulsive) when negative (resp. positive). Densities are shown in units of . In insets (a) and (b), a zoom of the regions delineated on the left panel, firstly in the small energies (long time) range, where the attraction is seen to be repulsive for smaller densities, because of the Coulomb repulsion (shown in red), and secondly for the densities in the area where the character of the interaction changes abruptly from attractive to repulsive (higher densities are shown in dotted lines). 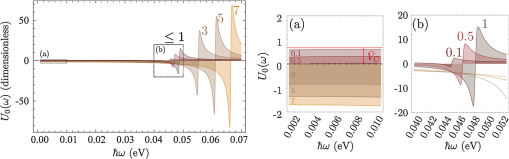 If we take instead of a quadratic dispersion for the excitation and assume all-excitonic interactions, , we can consider the same effect in the absence of a microcavity, relying on a purely excitonic (rather than polaritonic) BEC. In this case, the same procedure as detailed above leads to an effective potential as shown in Fig. 7. We kept all parameters the same for comparison except for the dipole moment, which we have taken three times as large (). This corresponds to the spatial separation of electrons and holes in the system of indirect excitons studied by Butov et al.38 The potential we obtain in the exciton case is very different in character from the polariton case, and is more closely related to the Cooper (conventional) shape of a square well, or the Bogoliubov potential including repulsive elbows.Fig. 7Same as Fig. 6 (also in units of ) but for the case of an exciton condensate. A larger dipole moment has also been assumed. The potential is different in character, much closer to Cooper’s potential with larger attraction at longer times. 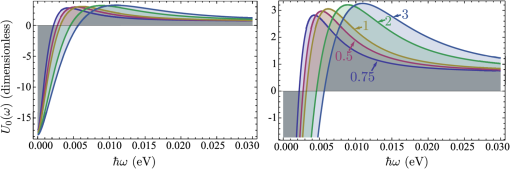 From these potentials, one can proceed to solve the gap equation. 4.Gap Equation4.1.Cooper PotentialThe BCS gap equation (2) is easier to tackle as a continuous equation: where we have also introduced a finite temperature from the Fermi-Dirac distribution of elementary excitations.52 With the BCS approximation of a step potential, the gap equation at zero temperature simplifies to . If , the dependence in the integral boundaries can be neglected (or, coming back to Eq. (2), one sees that in the initial gap equation, is exactly constant if and is zero otherwise). Thus, we can assume in this case the gap to be of the form: In this case, simplifying on both side of Eq. (24), we obtain:Equation (26) is better known as its approximation when , in which case it takes the form of the famous BCS gap expression, Solving exactly the gap equation calls for some numerical method. Equation (24) is a nonlinear integral equation, of the type studied by Hammerstein, i.e., where in our case and . There are strong conditions of existence of non-trivial (nonzero) solutions when ;53,54 however, the case when the kernel is not positive-definite, that is, in presence of repulsion,† has been much less studied mathematically.55 Cooper’s potential, being always negative, falls in the category of potentials which admit a unique non-trivial solution, with a stable numerical technique to obtain it, namely, since the mapping is contractive, by iterations of the gap equation: an initial (nonzero) function is used to compute the rhs of Eq. (24), providing which is injected back until the function converges. The gap computed in this way for a given Cooper potential is shown in Fig. 8(a). As one can see, the BCS approximation [Eq. (26)] remains a rather coarse approximation, since the gap turns out in this case to be bell-shaped rather than being a step function. Surprisingly, is however in much closer agreement with its approximation [Eq. (28)], as shown on Fig. 8(b) and 8(c) in the weak and strong coupling regime, respectively. There are small quantitative deviations in (b) between the numerical points and the formula when using the exact parameters of the potential. By fitting the numerical results, a perfect agreement can be found for slight variations of and . The BCS approximation therefore turns out to be an exceedingly good one as compared to an exact solution of the gap equation. For the procedure to make sense, similar results should be obtained for a smoothed well that approximates the BCS square well.41 We will not address this point here, but go directly to the case where the potential is not always attractive.Fig. 8Numerical solution to the gap equation with the BCS square well potential (a). The gap is not step-wise as approximated in the BCS model, but its value at zero exchanged energy, , is in close agreement with the analytical expressions, as seen in (b) and (c): as obtained from numerically solving the gap equation (dashed blue) and from Eq. (26) (solid magenta), (b) in the weak-coupling limit when , with small deviations as coupling is increased, and (c) in the strong-coupling where the agreement becomes perfect again. Note that increases linearly with the coupling strength out of the weak-coupling limit. 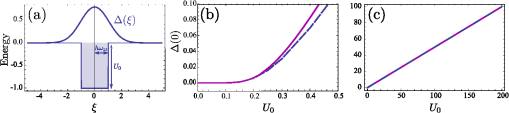 4.2.Bogoliubov PotentialThe potential is not always attractive when, for instance, some overall repulsion, such as direct Coulomb interaction, is superimposed on the attractive Cooper potential, as shown on Fig. 9. The Coulomb interaction is time independent and should therefore extend to all but here also a cutoff is introduced to avoid divergencies. This results in an attractive, Cooper-like potential, flanked by two repulsive windows. Such a potential is known as the Bogoliubov potential.56,57 Fig. 9Adding an overall repulsive Coulomb repulsion (red, left) until a cutoff to the BCS potential (green, left) results in the Bogoliubov step-wise potential (right). We take the convention , , positive in the above representation and , so that, e.g., means attractive contribution of the “Coulomb repulsion.”  This approximation has been used to show extremely counterintuitive behavior of the gap equation and justify a-posteriori another heavily criticized approximation of BCS, neglecting Coulomb repulsion: the BCS mechanism indeed assumes only attraction between electrons, which can be dimmed by Coulomb repulsion, but which never explicitly appears as such (like in the Bogoliubov scenario). The great result of Cooper was that binding occurs at arbitrarily small attraction. An important result of the Bogoliubov potential is to show that the detrimental effects of Coulomb repulsion are greatly reduced in the gap.57 We now present a linearization of the gap equation that allows one to obtain an approximate solution for the critical temperature.56 By assuming the gap equation to be a two-step valued function , the gap equation becomes with where appear invariably in the columns of . In Eq. (30a), the BCS approximation has been applied while in Eq. (30b), the fact that has been used to neglect in the denominator and the temperature in the numerator. The parametrization of the matrix in terms of the potential depends on the particular configuration (for example the relative widths of the various layers of the structure). Here we have adopted the original parametrization of Bogoliubov, which assumes narrow repulsive elbows surrounding a large attractive central region. Solving the linear equation for and then for the critical temperature, we find:In this form, one can see how Coulomb repulsion indeed introduces a small correction to the original BCS formula. The expression also seems to indicate that could be repulsive () and still lead to a gap as long as the denominator in Eq. (31) remains positive. In the following, we compare these predictions with numerical solutions of the gap equation, keeping in mind that the iterative procedure is not assured, mathematically, to converge. We have observed that indeed, it sometimes encounters problems and exhibits strong instabilities, with bifurcations of solutions, for example. In Fig. 10, we show the evolution of the gap function as is increased, from zero (BCS) to a point where the overall potential is essentially repulsive. With onset of the repulsion, the gap acquires two negative sides and becomes a highly distorted function for large . Note that the approximation of constant gap over the various regions is at least as good as for the case of BCS. Fig. 10Gap (thick magenta and, magnified, thick khaki) of the Bogoliubov potential (filled blue) solved numerically for the parameters: , , and taking values from (a) to (d) of: 0 (BCS), 0.1, 0.3 and 0.495. Coulomb repulsion results in a dip in the gap function that, for increasing values, results in oscillations in the gap function. Paradoxically, even when it is large and dominating attraction, repulsion does not prevent a gap, as seen in (d).  In Fig. 11, we now show the case where is held constant as the strength of the repulsion is varied independently. In foresight of what is to come later, we also allow the elbows to be negative, that is, to contribute an additional attraction to the conventional mechanism (for now we do not consider physical justification of this). Another unexpected result is obtained: the repulsive potential is in this case favoring a larger gap, as can be seen by comparing (a), where the gap function is highly oscillatory, to (d) where it recovers the BCS bell-shape. In (h), the distorted but overall attractive potential still results in a BCS type gap, but wider and larger. Note how the repulsion, by “squeezing” the gap, allows it to achieve much higher values than for the case of smaller or no repulsion. Fig. 11Gap (thick magenta and, magnified, thick khaki) of the Bogoliubov potential (filled blue) solved numerically for the following parameters: , , (fixed) and (the height of the elbow) taking values from (a) to (h) of: , , , 0 (BCS), 0.3, 0.5 (BCS), 1.5 and 5. The repulsive nature of the elbows change the character of the gap from bell-shaped to an oscillating function. The oscillating gap in the presence of strong repulsion allows, paradoxically, high values of the gap at zero-exchanged energy. 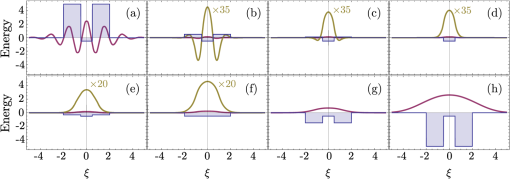 These unexpected results are confirmed phenomenologically by the Bogoliubov approximation Eq. (31), which reproduces qualitatively the trend of the gap as shown in Fig. 12. Here we should emphasize that the two quantities are not meant to be compared quantitatively, since one, (computed numerically) is the gap at zero temperature while the other, is the temperature at which the gap vanishes. There is a monotonous relationship between the two, that is, increasing implies increasing , so one can appreciate the consistency of the results by observing similar trends. The obstacle to conducting an extensive numerical comparison is that it is an intensive task numerically to compute , since this requires solution of the gap equation for various temperatures until the curve is obtained and its intersect with zero is found. A critical slowing down phenomenon makes the iterative process slower as the critical temperature is approached. In addition, numerical instabilities are stronger at nonzero . Therefore, although it is relatively straightforward to compute numerically, it is not convenient to use this method to obtain . On the other hand, the Bogoliubov approximation gives a fair estimate of , but is not able to provide the gap at zero temperature, since at the core of its method, there is an assumption of vanishing . Therefore, we have two complementary methods, each suited to provide a relevant aspect of the problem. We note that the gap at zero temperature is an important quantity which can be measured independently from by Andreev reflection in conductivity experiments. 4.3.Polariton PotentialIn the case of the polariton problem, we have seen that, even when neglecting Coulomb repulsion (as in the original BCS formulation), the potential departs strongly from the Cooper potential and features two large attractive regions far from small energies, immediately followed by two strong repulsive windows. We extend the Bogoliubov method to a three-step approximation of this potential, such as displayed in Fig. 13, with, in reference to previous potentials, notations , and for the boundaries of the central, shallow attractive region, narrow, deep attractive region and repulsive region, respectively. This is a notation only and is not mean to be understood as referring to Debye, Coulomb, or Bogoliubov in any strict sense. Following the same premises, we approximate the gap equation by a three-step valued function . This approximation turns out to be an exceedingly good one in certain cases, such as the one displayed in Fig. 13, where the gap itself is also a three-steps function in good approximation. Here there is even more room to choose a parametrization of the matrix. We now give general guidelines on how to build this matrix. The simplest method is to fix on the lhs of Eq. (25) at the center of each region and, in the corresponding row, take for each column the potential that is sampled more by the difference . Refinements are possible, such as weighting elements of by coefficients which reflect how much time the variables and spend in the regions that determine the matrix equation. This problem has the following mathematical expression: how is the random variable distributed when (resp. ) is uniformly distributed in an interval (resp. ). The solution is easily obtained as proportional (normalize to unity) to: This is easily obtained geometrically (the square root comes from Pythagoras’ theorem) and the problem results in finding the intersect of a line with the grid. There are two configurations. Working out the cases shows that Eq. (32) reduces to a triangular or a top-head truncated triangular distribution. The coefficients entering can then be taken as the potentials weighted by the area intersecting their corresponding region. The soundness of such an approach can be checked numerically to compare quantitatively various parametrizations. For simplicity, we shall here consider cases where only the dominant potential is considered. An example of such a gap equation is defined with: where and is integrated on the respective steps, as defined by the integral boundary conditions, i.e., .Fig. 13(solid blue) Three-step potential that models the form of effective electron-electron interaction when polariton-mediated with the three parameters and, (thick magenta) the gap as computed numerically for this potential. In good approximation, the gap is also itself a three-steps function. 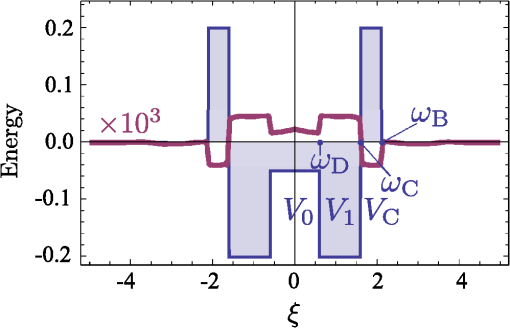 As before, we estimate the critical temperature by the condition that gives vanishing values of the gap on the whole interval. The first integral is evaluted in the same approximation as for the usual BCS (or Bogoliubov) potential: and are also essentially logarithmic in their energy range and we take: We solve the gap equation by setting its determinant to zero and solving for , giving We see that the impact of the polariton potential shape on the gap is rather intricate, here as well, with some unexpected behavior, produced both numerically and from this formula. In Fig. 14, we show the effect of widening the central, attractive region of the potential. Naively one would expect this to increase the gap (or critical temperature), since increases linearly with . However, Eq. (37) predicts a decrease of the critical temperature, as shown in Fig. 15. The reason why is understood by computing the gap at zero temperature, as seen in Fig. 14, where the repulsive barrier is shown to behave as a trap for the gap function, which results, as the width is increased, in a loosening of the gap strength, akin to the quantum mechanical situation of a bound state in a square potential. The numerical and linearized models display a good qualitative agreement, as seen in Fig. 15. Let us repeat that we are not considering here quantities that can be directly compared, since should be used for this purpose. Fig. 14Potential (filled blue) and its corresponding gap equation, solved numerically, as the size of the central attractive plateau is increased. Somewhat unexpectedly, the gap decreases as a result. The repulsive barriers have the effect of squeezing the gap up.  Fig. 15(joined points, blue) and (magenta) from the three-step Bogoliubov approximation, in the case where the width of the central attraction is increased. Unexpectedly, this results in a decrease of the critical temperature and of the gap. 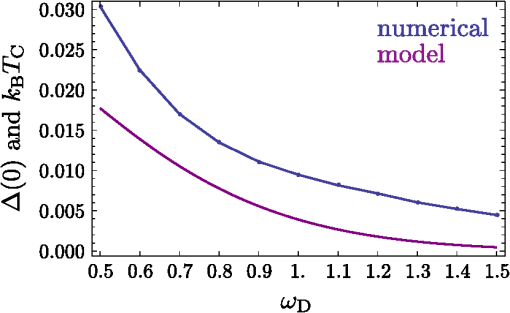 Another example is shown in Fig. 16, where both the attractive and repulsive parts of the potential are increased together. This results in a rapid increase of the gap. The result is also confirmed by numerical simulations, as shown in Fig. 17, and a good agreement is obtained. Unexpectedly, if the repulsive part grows twice as fast as the attractive one, not only does this also result in an increase of the gap, but even a faster one. This, too, is confirmed by the numerics. Note that in this case, we reach a region where our numerical procedure jumps to other solutions (usually of a highly oscillatory character, such as those reported in57), but behaves as expected until then. In this regard, the value of having an approximate analytical solution is obvious. Fig. 16Numerical solution of the gap equation when both the attractive and repulsive parts of the potential are increased together (here in the same proportions), showing a rapid increase of the gap. 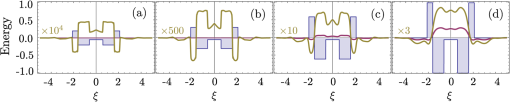 This analysis is finally applied to the case of the gap equation with the numerical results of the critical temperature obtained in both the polariton and exciton cases for the cases of Figs. 6 and 7. The parameters are gathered in Table 1 and the results plotted in Fig. 18. Both cases show a strong variation of the critical temperature with moderate variations of the condensate density (one order of magnitude). The polariton case is steeper and roughly linear while the exciton case increases less quickly but begins earlier. In both cases, temperatures are very high, and other effects will surely break the mechanism, for instance the loss of the condensate. This shows, however, the robustness of the mechanism in the conditions where it should apply. 5.ConclusionsWe have studied possible mechanisms of superconductivity in semiconductor heterostructure systems where a Bose–Einstein condensate mediating the effective electron-electron interaction leads to enhancement of the coupling, yielding very high critical temperatures. We have considered the case of an exciton-BEC, consisting of a sandwich of an -doped QW containing the superconducting electrons, in contact with coupled QWs where the BEC of indirect excitons is formed, for instance by optical excitation. We have also considered the case of a polariton BEC, where -doped QWs and undoped QWs hosting excitons are embedded in a microcavity. We have computed in these two cases the effective electron-electron interaction as a function of the exchanged energy , showing how the retardation effect acquires a peculiar character in the polariton case, namely, yielding a weakly attractive potential at long times, followed by a succession of strongly attractive and strongly repulsive windows. The gap equation in this case exhibits strong differences as opposed to the case of the Cooper potential (of conventional BCS and exciton-BEC mechanism). To understand the physical mechanism leading to large gaps and bypass numerical instabilities, we studied in detail the gap equation in the cases of simplified step-wise potentials, and offered an analytical method to obtain the critical temperature, which is in qualitative agreement with the numerical results. Our results suggest record-breaking critical temperatures in these systems. We stress, however, that the path toward achievement of exciton-mediated superconductivity at high temperatures may be long and full of obstacles. Of the two experimentally relevant systems that we have considered, one (coupled QWs) only shows the BEC of excitons at very low temperatures (less than 1 K 38). Consequently, one cannot expect high-temperature superconductivity in this system, although at low temperatures the superconducting gap may be very large. In microcavities, polariton BEC or polariton lasing have indeed been demonstrated at room-temperature.17,18 However, embedding a high-quality -doped QW inside the cavity, the proper choice of the experimental geometry in order to minimize optical absorption in the doped QW, and especially fabrication of quantum contacts for selective injection of carriers in the QW of interest, may pose technological difficulties. It is possible that hybrid metal-semiconductor or semi-metal-semiconductor systems may appear more suitable for the observation of the predicted effects. A conventional superconductor put in contact with a semiconductor also seems promising. Collective quantum phenomena in Bose–Fermi mixtures are extremely complicated and we foresee breakthroughs in their study in multi-layer structures combining a Fermi gas of electrons and an exciton-BEC. Notes*Note at this point that there is an error in Ref. 26 where only the direct exciton interaction has been taken into account with an incorrect power in the parenthesis, which led to an expression similar to the dipolar interaction. The direct interaction by itself turns out to be too small to evidence superconductivity with the parameters chosen in Ref. 26, therefore a dipole moment should be induced in this case, say by applying an external electric field, to restore the effect. AcknowledgmentsWe are grateful to H. Ouerdane and P. Lagoudakis for useful discussions. Support from EPSRC and EU FP7 ITN project CLERMONT4 are acknowledged. I.A.S. thanks the support from Icelandic National Research Council (Rannis) Center of Excellence in Polaritonics and FP7 IRSES POLAPHEN project. ReferencesA. Kavokinet al., Microcavities, 2nd ed.Oxford University Press, USA
(2011). Google Scholar
H. DengH. HaugY. Yamamoto,
“Exciton-polariton Bose–Einstein condensation,”
Rev. Mod. Phys., 82 1489
–1537
(2010). http://dx.doi.org/10.1103/RevModPhys.82.1489 RMPHAT 0034-6861 Google Scholar
A. Imamogluet al.,
“Nonequilibrium condensates lasers without inversion: exciton-polariton lasers,”
Phys. Rev. A, 53 4250
–4253
(1996). http://dx.doi.org/10.1103/PhysRevA.53.4250 PLRAAN 1050-2947 Google Scholar
J. J. Baumberget al.,
“Parametric oscillation in a vertical microcavity: a polariton condensate or micro-optical parametric oscillation,”
Phys. Rev. B, 62 R16247
–R16250
(2000). http://dx.doi.org/10.1103/PhysRevB.62.R16247 PRBMDO 1098-0121 Google Scholar
M. S. SkolnickT. A. FisherD. M. Whittaker,
“Strong coupling phenomena in quantum microcavity structures,”
Semicond. Sci. Technol., 13 645
–669
(1998). http://dx.doi.org/10.1088/0268-1242/13/7/003 SSTEET 0268-1242 Google Scholar
P. G. Savvidiset al.,
“Angle-resonant stimulated polariton amplifier,”
Phys. Rev. Lett., 84 1547
–1550
(2000). http://dx.doi.org/10.1103/PhysRevLett.84.1547 PRLTAO 0031-9007 Google Scholar
R. M. Stevensonet al.,
“Continuous wave observation of massive polariton redistribution by stimulated scattering in semiconductor microcavities,”
Phys. Rev. Lett., 85 3680
–3683
(2000). http://dx.doi.org/10.1103/PhysRevLett.85.3680 PRLTAO 0031-9007 Google Scholar
C. CiutiP. SchwendimannA. Quattropani,
“Parametric luminescence of microcavity polaritons,”
Phys. Rev. B, 63 041303(R)
–4
(2001). http://dx.doi.org/10.1103/PhysRevB.63.041303 PRBMDO 1098-0121 Google Scholar
C. CiutiI. Carusotto,
“Quantum fluid effects parametric instabilities in microcavities,”
Phys. Stat. Sol. B, 242 2224
–2245
(2005). http://dx.doi.org/10.1002/(ISSN)1521-3951 PSSBBD 0370-1972 Google Scholar
I. A. Shelykhet al.,
“Polarization propagation of polariton condensates,”
Phys. Rev. Lett., 97 066402
–4
(2006). http://dx.doi.org/10.1103/PhysRevLett.97.066402 PRLTAO 0031-9007 Google Scholar
A. KavokinG. MalpuechF. P. Laussy,
“Polariton laser polariton superfluidity in microcavities,”
Phys. Lett. A, 306 187
–199
(2003). http://dx.doi.org/10.1016/S0375-9601(02)01579-7 PYLAAG 0375-9601 Google Scholar
F. P. Laussyet al.,
“Spontaneous coherence buildup in a polariton laser,”
Phys. Rev. Lett., 93 016402
–4
(2004). http://dx.doi.org/10.1103/PhysRevLett.93.016402 PRLTAO 0031-9007 Google Scholar
M. H. SzymanskaJ. KeelingP. B. Littlewood,
“Nonequilibrium quantum condensation in an incoherently pumped dissipative system,”
Phys. Rev. Lett., 96 230602
–4
(2006). http://dx.doi.org/10.1103/PhysRevLett.96.230602 PRLTAO 0031-9007 Google Scholar
J. Kasprzaket al.,
“Bose–Einstein condensation of exciton polaritons,”
Nature, 443 409
–414
(2006). http://dx.doi.org/10.1038/nature05131 0028-0836 Google Scholar
R. Baliliet al.,
“Bose–Einstein condensation of microcavity polaritons in a trap,”
Science, 316 1007
–1010
(2007). http://dx.doi.org/10.1126/science.1140990 SCIEAS 0036-8075 Google Scholar
E. del Valleet al.,
“Dynamics of the formation and decay of coherence in a polariton condensate,”
Phys. Rev. Lett., 103 096404
–4
(2009). http://dx.doi.org/10.1103/PhysRevLett.103.096404 PRLTAO 0031-9007 Google Scholar
S. Christopouloset al.,
“Room-temperature polariton lasing in semiconductor microcavities,”
Phys. Rev. Lett., 98 126405
–4
(2007). http://dx.doi.org/10.1103/PhysRevLett.98.126405 PRLTAO 0031-9007 Google Scholar
J. J. Baumberget al.,
“Spontaneous polarization buildup in a room-temperature polariton laser,”
Phys. Rev. Lett., 101 136409
–4
(2008). http://dx.doi.org/10.1103/PhysRevLett.101.136409 PRLTAO 0031-9007 Google Scholar
A. Amoet al.,
“Collective fluid dynamics of a polariton condensate in a semiconductor microcavity,”
Nature, 457 291
–295
(2009). http://dx.doi.org/10.1038/nature07640 0028-0836 Google Scholar
D. Sanvittoet al.,
“Polariton condensates put in motion,”
Nanotechnology, 21 134025
–4
(2010). http://dx.doi.org/10.1088/0957-4484/21/13/134025 NNOTER 0957-4484 Google Scholar
A. Amoet al.,
“Superfluidity of polaritons in semiconductor microcavities,”
Nat. Phys., 5 805
–810
(2009). http://dx.doi.org/10.1038/nphys1364 NPAHAX 1745-2473 Google Scholar
K. G. Lagoudakiset al.,
“Quantized vortices in an exciton-polariton condensate,”
Nat. Phys., 4 706
–710
(2008). http://dx.doi.org/10.1038/nphys1051 NPAHAX 1745-2473 Google Scholar
K. G. Lagoudakiset al.,
“Observation of half-quantum vortices in an exciton-polariton condensate,”
Science, 326 974
–976
(2009). http://dx.doi.org/10.1126/science.1177980 SCIEAS 0036-8075 Google Scholar
D. Sanvittoet al.,
“Persistent currents quantized vortices in a polariton superfluid,”
Nat. Phys., 6 527
–533
(2010). http://dx.doi.org/10.1038/nphys1668 NPAHAX 1745-2473 Google Scholar
A. KavokinD. SolnyshkovG. Malpuech,
“Quatron-polaritons: charged quasi-particles having the bosonic statistics,”
Phys J. Condens. Matter, 19 295212
–8
(2007). https://doi.org/doi:10.1088/0953-8984/19/29/295212 JCOMEL 0953-8984 Google Scholar
F. P. LaussyA. V. KavokinI. A. Shelykh,
“Exciton-polariton mediated superconductivity,”
Phys. Rev. Lett., 104 106402
–4
(2010). http://dx.doi.org/10.1103/PhysRevLett.104.106402 PRLTAO 0031-9007 Google Scholar
L. N. Cooper,
“Bound electron pairs in a degenerate Fermi gas,”
Phys. Rev., 104 1189
–1190
(1956). http://dx.doi.org/10.1103/PhysRev.104.1189 PHRVAO 0031-899X Google Scholar
J. BardeenD. Pines,
“Electron-phonon interaction in metals,”
Phys. Rev., 99 1140
–1150
(1955). http://dx.doi.org/10.1103/PhysRev.99.1140 PHRVAO 0031-899X Google Scholar
J. Bardeen,
“Electron-vibration interactions superconductivity,”
Rev. Mod. Phys., 23 261
–270
(1951). http://dx.doi.org/10.1103/RevModPhys.23.261 RMPHAT 0034-6861 Google Scholar
A. J. Leggett, Quantum Liquids, Oxford University Press, USA
(2006). Google Scholar
J. BardeenL. N. CooperJ. R. Schrieffer,
“Microscopic theory of superconductivity,”
Phys. Rev., 106 162
–164
(1957). http://dx.doi.org/10.1103/PhysRev.106.162 PHRVAO 0031-899X Google Scholar
J. BardeenL. N. CooperJ. R. Schrieffer,
“Theory of superconductivity,”
Phys. Rev., 108 1175
–1204
(1957). http://dx.doi.org/10.1103/PhysRev.108.1175 PHRVAO 0031-899X Google Scholar
D. AllenderJ. BrayJ. Bardeen,
“Model for an exciton mechanism of superconductivity,”
Phys. Rev. B, 7 1020
–1029
(1973). http://dx.doi.org/10.1103/PhysRevB.7.1020 PRBMDO 1098-0121 Google Scholar
W. A. Little,
“Possibility of synthesizing an organic superconductor,”
Phys. Rev., 134 A1416
–A1424
(1964). http://dx.doi.org/10.1103/PhysRev.134.A1416 PHRVAO 0031-899X Google Scholar
V. L. Ginzburg,
“Проблема Высокотемпературной Сверхповодимости,”
Sov. Phys.-Usp., 13 335
–366
(1970). 0038-5670 Google Scholar
J. G. BednorzK. A. Müller,
“Possible high superconductivity in the Ba-La-Cu-O system,”
Phys. Z. B, 64 189
–193
(1986). http://dx.doi.org/10.1007/BF01303701 0722-3277 Google Scholar
A. J. Leggett,
“What do we know about high ?,”
Nat. Phys., 2 134
–136
(2006). http://dx.doi.org/10.1038/nphys254 NPAHAX 1745-2473 Google Scholar
L. V. Butovet al.,
“Towards Bose–Einstein condensation of excitons in potential traps,”
Nature, 417 47
–52
(2002). 0028-0836 Google Scholar
L. V. Butovet al.,
“Formation mechanism and low-temperature instability of exciton rings,”
Phys. Rev. Lett., 92 117404
–4
(2004). http://dx.doi.org/10.1103/PhysRevLett.92.117404 PRLTAO 0031-9007 Google Scholar
R. Rapaportet al.,
“Charge separation of dense two-dimensional electron-hole gases: mechanism for exciton ring pattern formation,”
Phys. Rev. Lett., 92 117405
–4
(2004). http://dx.doi.org/10.1103/PhysRevLett.92.117405 PRLTAO 0031-9007 Google Scholar
High-Temperature Superconductivity, Springer(1982). Google Scholar
P. MonthouxD. PinesG. G. Lonzarich,
“Superconductivity without phonons,”
Nature, 450 1177
(2007). http://dx.doi.org/10.1038/nature06480 0028-0836 Google Scholar
R. ButtéN. Grandjean,
“A novel class of coherent light emitters: polariton lasers,”
Semicond. Sci. Technol., 26 014030
–9
(2010). http://dx.doi.org/10.1088/0268-1242/26/1/014030 SSTEET 0268-1242 Google Scholar
H. Ouerdaneet al.,
“Photon emission induced by elastic exciton-carrier scattering in semiconductor quantum wells,”
Eur. Phys. J. B, 65 195
–206
(2008). http://dx.doi.org/10.1140/epjb/e2008-00355-x EPJBFY 1434-6028 Google Scholar
H. Ouerdane,
“Analytic model of effective screened coulomb interactions in a multilayer system,”
J. Appl. Phys., 110 074905
–9
(2011). http://dx.doi.org/10.1063/1.3646482 JAPIAU 0021-8979 Google Scholar
F. TassoneY. Yamamoto,
“Exciton-exciton scattering dynamics in a semiconductor microcavity stimulated scattering into polaritons,”
Phys. Rev. B, 59 10830
–10842
(1999). http://dx.doi.org/10.1103/PhysRevB.59.10830 PRBMDO 1098-0121 Google Scholar
M. J. BijlsmaB. A. HeringaH. T. C. Stoof,
“Phonon exchange in dilute Fermi–Bose mixtures: tailoring the fermi-fermi interaction,”
Phys. Rev. A, 61 053601
–10
(2000). http://dx.doi.org/10.1103/PhysRevA.61.053601 PLRAAN 1050-2947 Google Scholar
V. L. Ginzburg, On Superconductivity and Superfluidity, Springer(2009). Google Scholar
I. A. ShelykhT. TaylorA. V. Kavokin,
“Rotons in a hybrid Bose-Fermi system,”
Phys. Rev. Lett., 105 140402
–4
(2010). http://dx.doi.org/10.1103/PhysRevLett.105.140402 PRLTAO 0031-9007 Google Scholar
W. J. Thompson,
“Principal-value integrals by a simple accurate finite-interval method,”
Comput. Phys., 12 94
–96
(1998). http://dx.doi.org/10.1063/1.168641 CPHYE2 0894-1866 Google Scholar
J. V. Noble,
“Gauss-legendre principal value integration,”
Comput. Sci. Eng., 2 92
–95
(2000). http://dx.doi.org/10.1109/MCISE.2000.970778 CSENFA 1521-9615 Google Scholar
P. G. de Gennes, Superconductivity of Metals Alloys, Addison-Wesley, Redwood City, CA
(1989). Google Scholar
M. Kitamura,
“Non-linear integral equations of the Hammerstein type,”
Prog. Phys. Th., 30 435
–442
(1963). http://dx.doi.org/10.1143/PTP.30.435 Google Scholar
A. Vansevenant,
“The gap equation in superconductivity theory,”
Physica D, 17 339
–344
(1985). http://dx.doi.org/10.1016/0167-2789(85)90217-9 PDNPDT 0167-2789 Google Scholar
P. P. ZabreikoA. I. Povolotskii,
“On the theory of the Hammerstein equation,”
Ukrainian Mathematical Journal, 22 127
–138
(1970). http://dx.doi.org/10.1007/BF01125601 UKMJB6 0041-5995 Google Scholar
J. B. KettersonS. N. Song, Superconductivity, Cambridge University Press, Cambridge
(1999). Google Scholar
X. H. ZhengD. G. Walmsley,
“Coulomb repulsion in BCS theory of superconductivity,”
Phys. Rev. B, 71 134512
–9
(2005). http://dx.doi.org/10.1103/PhysRevB.71.134512 PRBMDO 1098-0121 Google Scholar
Biography Fabrice P. Laussy is a French theorist of quantum light-matter interactions. He made significant contributions to the theory of polariton lasers, Bose condensation and superfluidity of exciton-polaritons. PhD of Université Blaise Pascal, Clermont-Ferrand, 2005, under the supervision of Alexey Kavokin, research associate at the University of Sheffield (United Kingdom), 2006, at the Universidad Autónoma de Madrid (Spain), 2007, and at the University of Southampton (UK), 2008 to 2009. Presently a Marie Curie fellow in the Walter Schottky Institut of the Technische UniversitätMünchen, Germany. Coauthor of Microcavities (OUP 2007, 2011).  Thomas Taylor is a British PhD student of Alexey V. Kavokin at the University of Southampton, UK (2009–present). Graduated with an MMathPhys in mathematics and physics from the University of Warwick (2004 to 2008).  Ivan. A. Shelykh is a Russian and Icelandic theoretical physicist expert in solid state optics and mesoscopic transport, coordinator of the Icelandic “Center of Excellence in Polaritonics”. Graduated from the Saint Petersburg Polytechnical University in 1999. Received PhD in 2001 from the same institute. Visiting professor in the International Center of Condensed Matter Physics, Brasilia, Brazil (2006 to 2008). Currently employed as professor at the University of Iceland and Nanyang Technological University, Singapore.  Alexey V. Kavokin is a Russian and French theoretical physicist expert in solid state optics and semiconductor physics, head of the Spin Optics Laboratory (SOLAB) in Saint-Petersburg, coordinator of the series of EU Research-Training networks “Clermont” and Scientific Director of the Mediterranean Institute of Fundamental Physics (MIFP). Graduated from the Saint Petersburg Polytechnical University in 1991. Member of staff of the Ioffe Physico-Technical institute (1992 to 2000). Graduated from the Ioffe Physico- Technical institute, in 1993, with a PhD in physics and mathematics (supervisor Prof. E.L. Ivchenko). Professor at the Blaise Pascal University (Clermont-Ferrand, France, 1998 to 2005). Currently Chair of Nanophysics and Photonics at the University of Southampton (Southampton, UK, 2005-present). Co-author of the textbooks Cavity polaritons (Elsevier 2003) and Microcavities (OUP 2007, 2011). |