|
|
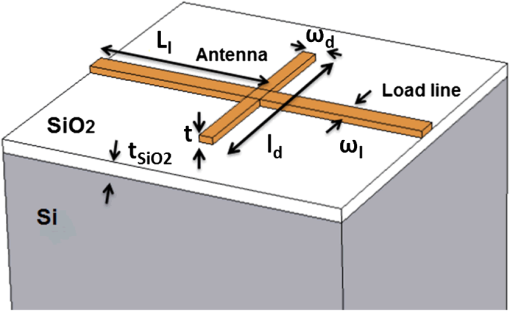
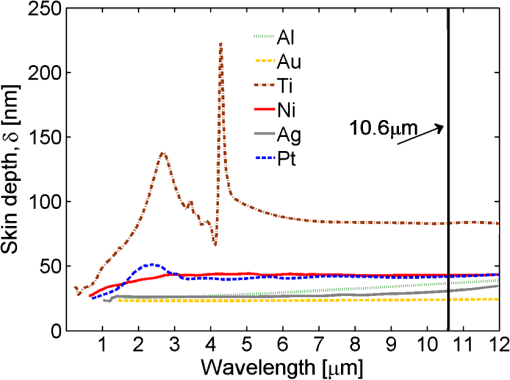
1.IntroductionThe use of metallic structures resonating at optical frequencies is drawing a great deal of attention within the nanoscience and nanotechnology communities. These structures have paved the way for new kinds of optical elements able to modify the spectral, polarization, and phase characteristics of an incoming optical wavefront, allowing the emergence of the area of resonant optics. Besides, these structures can be used to enhance the electric field by several orders of magnitude while maintaining a high spatial resolution. Very interesting applications have appeared in a variety of areas: infrared antenna-coupled detectors, biomedical applications, photonic materials, field enhancement, and energy harvesting.1–8 Their response is intrinsically selective to frequency, incidence conditions, and state of polarization of the incoming electromagnetic wavefront. The performance of these devices, which we name here as optical nanoantennas, is strongly dependent on their geometry, as it happens with their low-frequency versions. However, metals at optical frequencies stop behaving as perfect conductors and their dispersive characteristics begin to play a decisive role. When used as optical detectors in the visible or the infrared,3,9–11 the electric currents generated by the incoming electromagnetic field are rectified by nonlinear rectifying elements, such as metal–oxide–metal or metal–insulator–insulator–metal junctions,12,13 or dissipated as heat within the structure and surrounding media. In this contribution, we focus our attention on this last type of dissipative transduction mechanism, where the Joule effect produces a change in temperature that varies the resistance of the materials. This behavior is known as the bolometric effect. Most micro-bolometric antenna-coupled detectors are configured as having a resonant element, or a radiation collector, that redirects the heat transfer towards a nanometer-size bolometer. In most cases, the bolometric material is different than the material used for the antenna or collecting structure. This nanobolometer usually presents a good thermal isolation, a high resistance and also a large value of the temperature coefficient of resistance (TCR). This nanobolometer is in-chip connected to the signal extraction lines and also receives the currents generated by the resonant structures. However, when analyzing the bolometric constant of the material typically used with this configuration, we find that the values of the available metals used both for the antenna and nanobolometer are very similar. Therefore, some advantages can be taken from an approach where the whole antenna structure works as a bolometric element. This has been called a distributed bolometer configuration.11 This approach allows a simpler, and cheaper, fabrication method where only one material is used both for the resonant structure and the bolometer, avoiding two-material devices that are prone to fabrication errors due to miss-alignment and lack of homogeneity.3,11 The price paid for simplicity in distributed bolometric devices is a lower response thancan be obtained from a two-material device composed of a nanobolometer coupled to an antenna. The design procedure of optical antennas typically uses numerical electromagnetic software packages for the simulation of the involved structures. Computational electromagnetics offers a wide variety of methods that the designer has to evaluate to choose the best one for the given problem. In this area, the similarity between the results obtained in the simulation and those obtained by testing the fabricated devices is quite remarkable and increases the reliability of the proposed designs. In the case of distributed bolometers, the devices must also be analyzed from the thermal point of view. Therefore, the analysis of the results obtained from the simulation packages have to be properly interlinked to faithfully represent the given case. Then, the simulation of these devices becomes a multiphysics problem. Researchers and engineers have been using several computational electromagnetics packages such as HFSS, CST Microwave Studio, and COMSOL Multiphysics.14 Our choice for the current problem is the Finite Element Method software COMSOL Multiphysics. It provides a good multiphysics platform where both the electromagnetic and thermal domains are fully integrated. After obtaining the results for the temperature change produced by the optical radiation, the analysis should focus on how the device converts this difference into a change in the electric signal. Then, the final output produced by the device also depends on the electric wiring and circuits used to extract the signal. All these parameters, optical, thermal, and electrical have to be combined to increase the performance of the proposed devices. Our simulation considers a plane-wave inciding normally on the antenna structure with a polarization state that is parallel or perpendicular to the dipole orientation. The results obtained here can be extended to simulate other conditions of incidence.15,16 In this paper we have considered most of the elements contributing to the signal, ranging from the choice of the metal used to fabricated the resonant structures, to the values of the resistance of the electric circuit that delivers the output signal. Some previous papers have analyzed the role of the geometry of optical antennas and the effect of the substrate.16–19 However, as far as we know, there are no interlinked analyses of the various subsystems around a working antenna-coupled bolometer. Section 2 presents the physical mechanisms involved in the analysis of the performance of distributed bolometers coupled to optical antennas. These devices are fully considered in Sec. 3 where we have described the geometry and surrounding elements of the device, along with the definition of the main parameters that are optimized along the analysis. Section 4 shows the results of the optimization and suggests several strategies to obtain a more efficient design. Finally, Sec. 5 summarizes the main conclusions of this paper. 2.Multiphysics ApproachWhen an electromagnetic wave interacts with resonant metallic structures such as those analyzed in this paper, there are several physical mechanism that trigger the signal or response of the device. For a nanoantenna working as a distributed bolometer, electromagnetism and heat transfer will play the most significant roles in the description of the element.11,20 This double contribution, thermal and electromagnetic, combines into a multiphysics model. In some areas of interest this multiphysics approach is expanded to include mechanical vibration.21 From the electromagnetic point of view, the antenna couples the incoming electromagnetic radiation into the metallic structure. The first effect is to build electric currents up that flow through the device, concentrate on the feed point of the antenna and, consequently, increase its temperature. This increase in temperature follows a spatial distribution that depends on the material properties, both from the electromagnetic and thermal domains, and the geometry. In a previous contribution we reported that the simulated results agreed with the experimental data for two different kinds of dipole antennas.11 Once the temperature changes, the bolometric effect induces a change in the resistivity that is finally detected by an external circuit. We begin this description within the thermal domain. The heating of the device is described by the Joule effect. The power dissipated by the antenna structure is seen as a heat source.11,22,23 The total heat produced after excitation is given by the following relation: where is the conductivity of the metal at the frequency of the incident wave, is the spatial distribution of the electric field of the electromagnetic wave, and is the antenna volume. The electric field distribution, , is obtained after solving the following wave equation: where the imaginary term, , is related with the absorption of the metal, is the wave-number, and is the relative magnetic permeability.To find out the change in temperature of the metal structure we need to use the heat transfer equation: where is the mass density, is the heat capacity, is the thermal conductivity and is the power heat density (), which is related with the power dissipation given in Eq. (1). The detection set-up of a bolometric optical antenna uses a modulated optical signal (mechanical or electronically driven) with modulation frequencies in the range of the KHz. Because of the small mass associated with the size of the optical antenna, the thermal inertia is quite low and the system quickly reaches a stationary regime. This fact makes possible to neglect the left-hand side of Eq. (3). Therefore, in this study, the mass density, , and heat capacity, , are not of importance.The change in temperature causes a change in the resistance of the device. This change is described by the following equation: where is the cross-section of the device, is the resistivity at a temperature , is the TCR, and is the distribution of the temperature change along the length of the device. The length used in this calculation is because we take into account the length of the load lines that extract the signal toward an external circuit.3.Optical Antennas as Distributed BolometersAs we have seen in the previous section, optical antennas can produce a signal using the bolometric effect. Typically, a bolometric optical antenna contains a nanobolometer located at the feed point of the antenna. The material of the bolometer is typically selected as having the maximum available value of , along with good conductive behavior. This configuration has been proved and demonstrated experimentally in the infrared. However, this approach requires two e-beam lithographies involving two material deposition along with tight spatial alignment constraints. A proposal to ease the fabrication of bolometric optical antennas has been made. It takes advantage of similarities in value of among the metals typically used in the fabrication of optical antennas. Then, the whole resonant structure works as a distributed bolometer. In this case, the simulation needs both the thermal and electromagnetic domain to fully describe the device. The main parameters of the design can be classified in two different categories: geometric and material parameters. From the geometric point of view, the main factors are the spatial dimensions together with the shape of the antenna, and the load lines extracting the signal. The optical and thermal constants of the materials used to fabricate the system are also of great importance. Besides, the surroundings of the resonant element play a decisive role both from the electromagnetic and thermal domains. The parameters of the surroundings are also the materials and the thickness of the insulator layers used in the device. The geometrical set-up to connect the antenna to the load line is important when considering the electromagnetic resonance of the device. For example if the antenna is aligned to the load lines, the geometry is more of a resonant wire. This configuration shifts the resonance towards lower frequencies. In this paper we have selected a geometry where the antenna is perpendicular to the load lines. In our case, we can decouple the electromagnetic resonance from the spurious and parasitic resonance of the load line just by aligning the electric field along the dipole. Figure 1 shows the main spatial dimensions of a dipole optical antenna. These geometrical parameters are the length of the dipole, , its width, , and thickness, . The geometry of the load lines is also given by its length, , and width, . We assume that the thickness of the load lines is equal to the thickness of the dipole. This is because the fabrication is made with the same deposition process. The value of has been fixed to 15 μm for all the devices considered in this paper. From a material point of view, the dipole is fabricated with a metal having a complex index of refraction, , being the angular frequency of the optical radiation. Electromagnetically, the metal also shows a high frequency conductivity, . These parameters are related by the following equation: where is the real part of the relative dielectric permittivity of the material.22 An important value of the material is given by the penetration depth:Depending on the value of we can optimize the thickness of the dipole, , to accommodate better the currents flowing within the material. Besides the electromagnetic characteristics, the thermal properties of the materials are mainly described by the thermal conductivity , its specific heat, , and the mass density, . In Sec. 2, we have seen that the system behaves as stationary. Therefore, and are not included as design parameters. Figure 2 shows the spectral variations of the skin depth for several metals. We can see that Ti shows the largest value of skin depth. This means that the electric field penetrates deeper into the metal, building up electric currents within it. This property will be fully exploited when simulating the overall response of devices fabricated in Ti. On the contrary, Au is the metal showing the thinnest skin depth. On the other hand, skin depth will also affect the optimum resonant length of the dipole. It is known that the length of the dipole, , at which the maximum response is obtained, , depends on the value of the index of refraction of the surrounding materials. This has been demonstrated by Novotny24 using the concept of effective wavelength, . This is the wavelength at which the antenna resonates, and follows the linear relation: where and are constants derived from material and geometric characteristics, describes the plasmon resonance, and is the wavelength in vacuum. The concept of effective wavelength can be also described classically when the resonant structure is between two media, as it happens with the elements considered in this paper. In this case, the effective wavelength is given as where and are the dielectric permittivity of and vacuum respectively. However, when simulating the response of the device we can parameterize it with respect to the skin depth of the material. The result (see Fig. 3) shows that shorter dipoles are better for a larger skin depth, as expected from previous published results.8,11 Because of manufacture tolerances, this effect seems a disadvantage when considering Titanium as a construction material for optical antennas. However, as we will see in the next section, the resonant length and the total response of the device also depends on the antenna thickness, which can be tailored according to the material’s characteristics.Fig. 3Optimum resonant length, of a dipole antenna as a function of the skin depth. The antenna is assumed to be on a Si wafer coated with a layer of and having a thickness . 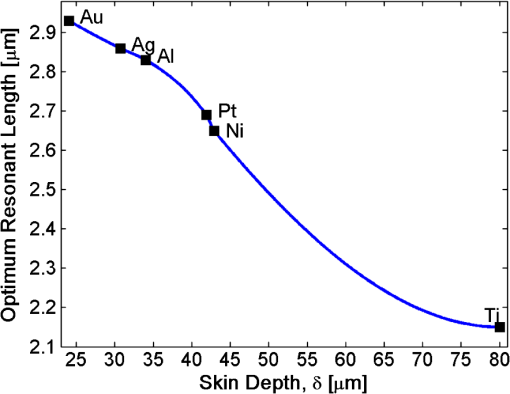 The thermoelectric behavior will be governed by electric resistivity at low frequencies, , and the TCR parameter, . Table 1 summarizes the electromagnetic and thermal parameters for several metals of interest analyzed in this paper.25–27 Table 1Electromagnetic and thermal properties of metals.
The previous discussion dealt with the characteristics of the resonant element. Now we are interested in knowing how the surrounding may affect the performance of the device. We have already seen how the optical properties of the layer changes the value of the effective wavelength [see Eq. (7)]. Optically, the thickness of this layer is a fraction of the wavelength and produces multiple beam interferences that determine the distribution of light at the plane of the antenna. Besides, this material is a good thermal insulator that diminishes the leakage of heat from the resonant element to the substrate, allowing the temperature to increase. Another important subsystem of a bolometric optical antenna is the external circuit used to extract the signal generated by the device. If a voltage source is used to bias the device, the external circuit takes the form of a voltage divider (see Fig. 4). The bolometric antenna, having a resistance , is in series with an additional resistance caused by the in-chip connection, . Besides, an external resistance, , completes the voltage divider. Actually, can be varied to locate the bias voltage at the working point and also to limit the DC current flowing through the bolometer. The DC voltage obtained from the divider is where is the voltage given by the bias source, and is the DC voltage obtained from the device. As far as the incidence of light will change the resistance of the antenna, , the response of the device to the incoming radiation is a change, , in the value of , that is given as where we can see how the in-chip and external resistance are of importance in the final signal of the device. This equation is valid when . This condition is fulfilled in the case of the distributed bolometer treated here.Fig. 4Schematics of two possible biasing circuits: voltage bias (a) and current bias (b). The antenna is denoted as . is the resistance of the signal extraction lines included in the chip. is the resistance used to fix the bias voltage in the voltage source configuration. 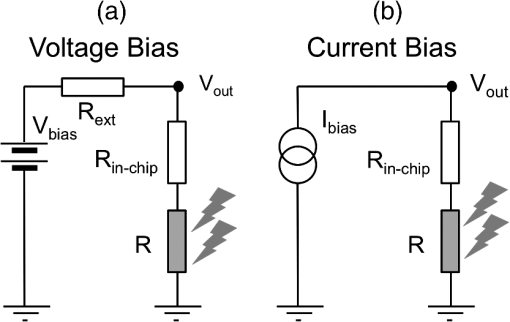 At the same time, the electronic set-up can be simplified to include a current source [see Fig. 4(b)]. In this case, the signal becomes where is the current delivered by the source and is given by Eq. (4). This case will be analyzed more deeply in Sec. 4.4.ResultsIn this section, we focus our attention on the optimization of the behavior of the bolometric optical antenna as a function of the selected material and the geometric parameters involved in it. The response of the devices is produced when a plane wave is incident normally to the wafer, having a polarization oriented along the direction of the dipole, and with a power density of at a wavelength of . 4.1.Density Current DistributionAn interesting result of this analysis is presented in Table 2, where we have calculated the power absorption for optical antennas fabricated with different materials and having an optimum dimension in length (see Fig. 3). Table 2 shows that Ti, having the largest skin depth, shows the highest power absorption because the electric field is able to penetrate deeper into the structure and generate currents within a larger volume than other materials. We can also conclude that when metals show similar skin depth values, the metal showing the largest electric conductivity performs better. We have already checked how the resonant length of the optimum dipole antenna, , depends on the choice of the material (see Fig. 3). However, in addition, the thickness of the dipole changes the length for an optimum response. In this case we find that the length should be longer as the thickness increase. Figure 5(a) shows this dependence for the case of Titanium. Besides, Fig. 5(b) shows the transversal distribution of the current density for a plane located at the feed point of the antenna. The current density fills better a thinner device. From Tables 1 and 2, we may see that when the skin depth, , is similar, then the absorbed power is larger as the conductivity, , increases. Table 2loptimum and power absorption.
Fig. 5(a) Dependence of the resonant length of a Ti dipole antenna as a function of the thickness. (b) Distribution of the transversal current density at the feed point of a Ti antenna for three values of the thickness of the device: 100, 200, and 350 nm. A darker map means a larger value of the current density, . 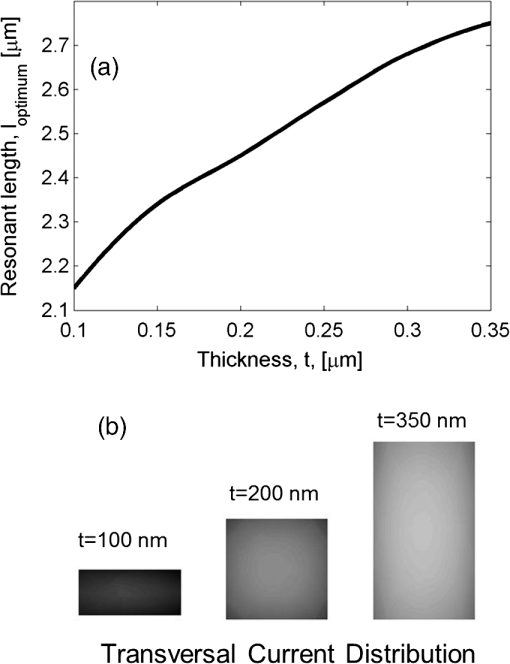 4.2.Temperature DistributionFrom the thermal point of view, we have seen that the main physical parameter is the value of the thermal conductivity, . In our analysis we have seen that Ti shows the smallest thermal conductivity among the studied metals (see Table 1). This fact produces a stronger concentration of heat in the optical antenna and its surroundings, including the load lines. In Fig. 6(a), we show the temperature profile for the geometry given in Fig. 1, for different optical antennas having a length that has been optimized (see Table 2). Au shows an almost flat temperature profile due to its large value of the thermal conductivity. This behavior can be of great interest when applying resonant structures for localized heating of biological or micromechanical structures.21,28 At the same time, due to the thermal conduction of the load lines we have analyzed the dependence of the temperature difference as a function of the width of the load lines [see Fig. 6(b)]. As expected, a wider load line resulted in a lower temperature difference, producing a weaker signal in the output circuit. At the same time, Table 3 shows the change in signal produced by a Ti antenna having an optimized length, , and a thickness as a function of the width of the load line, . Fig. 6Temperature distribution along the load lines for a dipole optical antenna having an optimum resonant length of the dipole, as a function of the material used to fabricate the resonant structure (a), and (b) as a function of the width of the load line, , for an Al antenna having the optimum length. 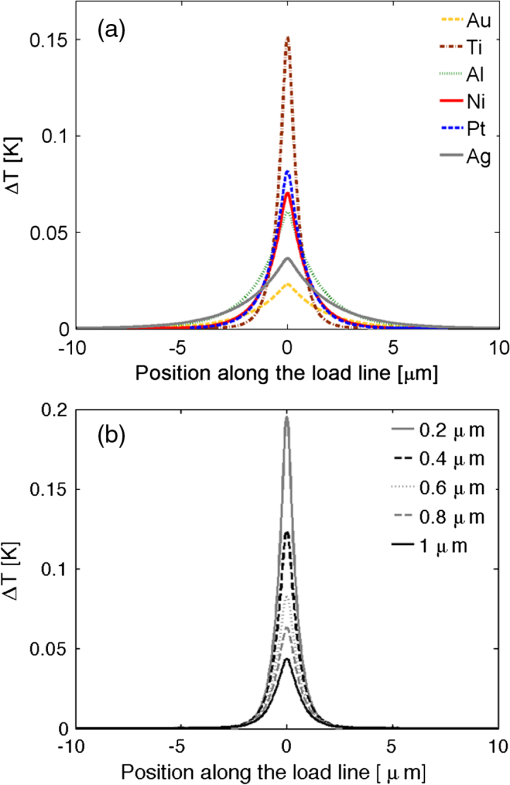 Table 3ΔVout versus ωl.
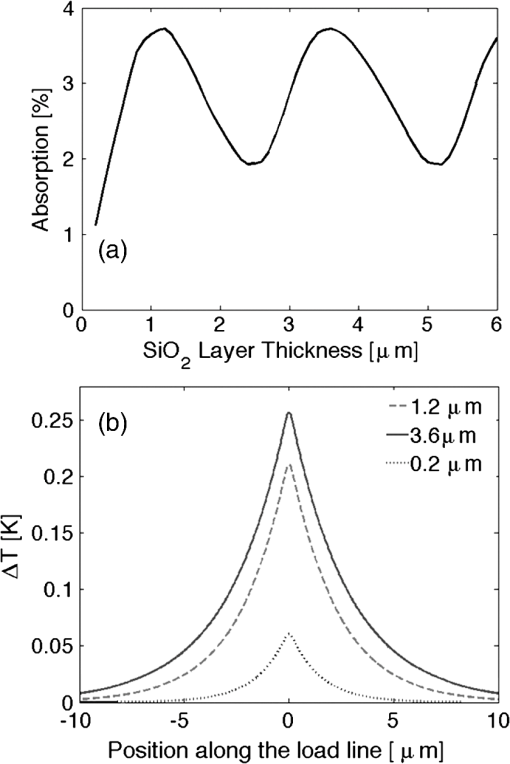
4.3.TCR ParameterWe have seen that the temperature difference causes a change in the resistivity of the device, which is sensed by the external circuit. As far as the resistivity changes linearly with changes in temperature, the signal obtained from the device is linearly proportional to the value of the TCR of the material. However, this proportionality only holds when considering the same temperature difference. As we have seen previously, this temperature difference, and its distribution along the device, changes with the geometry and the material selected for the structure. Therefore, it is not possible to ensure that a material with 50% larger value of the TCR than another material, will perform with an output signal 50% higher. 4.4.Insulating LayerThe thickness of the layer plays an important role from the electromagnetic and thermal point of view. It produces constructive or destructive interferential effects depending on the relation between the wavelength of illumination, the thickness, the angle of incidence, and the state of polarization for non-normal incidence conditions. For the wavelength of resonance, and normal incidence conditions, the effect on the absorption is periodic with respect to the thickness. At the same time, is a thermal insulator and, for our case, the thicker the layer the better the insulation is, and a larger temperature difference is observed because heat cannot flow through the substrate. These two effects can be seen in Fig. 7 where the power absorption of the device and the temperature distribution along the load lines are plotted as a function of the thickness of the layer. From the thermal point of view, we have found that after a thickness of , no improvement is observed by having a thicker layer, because the oscillation in the absorbed power due to optical multiple-beam interferences are more significant. Besides, there are limits for a reliable fabrication of layers thicker than 2 to 3 μm. 4.5.Biasing CircuitAnother important issue related to the practical use of bolometric optical antennas is the choice between a voltage source or a current source. Although voltage sources have been typically used in most laboratory systems, current sources are a better choice when all the electric parameters are set and an improvement in the performance and reliability of the signal is desired. For a voltage source an interesting result is obtained when considering the dependence of the signal versus the value of the in-chip resistance, . This value depends on the material choice as well as the actual geometry of the load lines and signal extraction lines from the device to the external circuit. Therefore, we may see how this auxiliary feature is affecting the value of the final signal. Figure 8(a) shows this dependence when different materials are used. We can see that Ti behaves better for lower values of , and Ni produces a larger signal when is higher than 400 ohms. At the same time, we have analyzed in Fig. 8(b) the dependence of the signal with respect to the resistance of the external circuit, . Using Eq. (9), we have calculated the signal as a function of for different materials. Again, Ti provides a larger signal when the external resistance is larger than . The parameters fixed in this analysis have been the geometry of the device, and the thickness. Figure 8 shows that there exist an optimum value of the external resistance providing the largest response for a given material. The value of this optimum resistance fixes the voltage applied to the device. This voltage needs to be below a damage threshold value to avoid the destruction of the device.29 Fig. 8(a) Response of the device as a function of the in-chip resistance, , for different materials. (b) Response of the device as a function of the external circuit resistance, , for different materials. 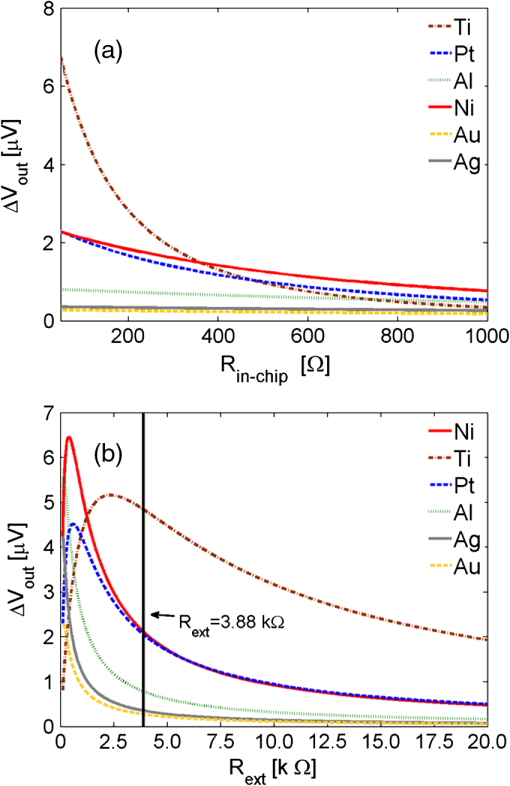 In Table 4 we compare the response of different antennas fabricated with different materials but having an optimum length of the dipole. The width of the load lines and thickness are the same for all the devices: and . The thickness of the layer is also 0.2 μm. The three columns represent three biasing situations: a voltage source at , a voltage source producing the same value of the DC current flowing through an optimized Au antenna, and a current source with the same value of the DC biasing current than the previous case. We may see how the Ti antenna provides the strongest signal for a bias current configuration. Table 4Comparison for three cases of biasing points.
4.6.OptimizationWe have analyzed how the parameters of the system can be selected to optimize the performance of the device at . Taking into account the results obtained here the optimum structure is a Ti antenna with 2.2 μm in length, 0.1 μm in thickness and 0.2 μm in width. The load line should be perpendicular to the antenna and having a width of 0.2 μm. The value of is taken for practical manufacture considerations. Considering the typical configuration of Si wafers, the insulator layer should be made of and having a thickness of 1.2 μm. The bias circuit should use a current source. Table 5 compares the optimized structure with a gold distributed bolometer.3,9,11,15 The change in temperature for the optimized structure is significantly higher than the temperature of the gold structure, presenting a bolometric response almost 3 orders of magnitude larger. Table 5Comparison in performance for two different antennas.
5.ConclusionsIn this contribution, we have demonstrated that, in order to make a complete representation of an optical antenna, a multiphysics simulation approach is needed to combine the effect of the electromagnetic wave building currents within the resonant structure, and the heat transport along it. The change in temperature also induces a change in resistivity that is finally sensed by dedicated electronic circuitry. The case treated here is a distributed bolometer where the bolometric effect is not confined at the feed point of the antenna, but is distributed along the whole resonant structure and load lines. The results obtained here, although obtained in the infrared, can be properly extended to the visible range, just by considering the metal properties at visible frequencies along with the substrate materials supporting the devices. We have analyzed how different metals can be chosen taken into account the results obtained from simulation. We have identified the main geometric parameters of the design and how these are changed according to the material choice. From this multiphysics analysis we could check how the behavior of optical antennas differs from the classic response for perfect metal antennas. Some of the parameters considered here (load line geometry, isolation layer thickness, biasing circuit) are seldom treated. However, a fine tuning of their values can improve the overall performance of the device. As far as multiphysics simulation can be considered as a reliable design method, very precious time and resources are saved by a sound numerical simulation approach. However, we should not forget that the results obtained from real fabricated devices are the final proof of any analysis. Summarizing the main findings of this contribution, we may say that to obtain a stronger response from a distributed bolometric optical antenna, we should select a material having a large value of the skin depth. In this case, the field penetrates deeper within the antenna and the currents generated there dissipate better as heat. We have checked that the optimum resonant length of the dipole is shorter when materials with a larger skin depth are considered. This optimum resonant length also increases proportionally to the thickness of the device. When the values of the skin depth are alike, the driving parameter is the electric conductivity, . Selecting a material with larger conductivity increases the power absorption of the device. This absorption also occurs when the antenna is much thicker than the skin depth. The analysis in the thermal domain suggests that the response is higher for materials having a smaller thermal conductivity. The load lines, auxiliary to the device, should be narrow to concentrate the heat around the feed point of the antenna, producing a larger change in temperature. The insulating layer behaves as an optical coating showing a periodic behavior with thickness. From the thermal point of view, a layer thicker than 1.2 μm is not advantageous. The biasing circuit for improved performance should use a current source. For a voltage source, as those used in some previous experiments, there exist a value of the external resistance that maximizes the response. At the same time, the lower the resistance of the in-chip connections, the stronger the signal is. Finally, we have obtained an optimized device that produces an output signal stronger than a reference Au dipole of the type used in previous experiments. AcknowledgmentsThis research has been possible thanks to the project ENE2009-14340 funded by the Ministerio de Ciencia e Innovación of Spain. ReferencesK. B. Croizieret al.,
“Optical antennas: resonators for local field enhancement,”
J. Appl. Phys., 94
(7), 4633
–4641
(2003). http://dx.doi.org/10.1063/1.1602956 JAPIAU 0021-8979 Google Scholar
R. CorkishM. A. GreenT. Puzzer,
“Solar energy collection by antennas,”
Sol. Energy, 73
(6), 395
–401
(2002). http://dx.doi.org/10.1016/S0038-092X(03)00033-1 SRENA4 0038-092X Google Scholar
F. J. GonzálezG. D. Boreman,
“Comparison of dipole, bowtie, spiral and log-periodic IR antennas,”
Infrared Phys. Technol., 46
(5), 418
–428
(2005). http://dx.doi.org/10.1016/j.infrared.2004.09.002 IPTEEY 1350-4495 Google Scholar
J. Aldaet al.,
“Optical antennas for nano-photonic applications,”
Nanotechnology, 16 S230
–S234
(2005). http://dx.doi.org/10.1088/0957-4484/16/5/017 NNOTER 0957-4484 Google Scholar
S. A. Maier,
“Plasmonics: metal nanostructures for subwavelength photonic devices,”
IEEE J. Sel. Topic Quantum Electron., 12
(6), 1214
–1220
(2006). http://dx.doi.org/10.1109/JSTQE.2006.879582 IJSQEN 1077-260X Google Scholar
L. Tanget al.,
“Nanometre-scale germanium photodetector enhanced by a near-infrared dipole antenna,”
Nat. Photonics, 2 226
–229
(2008). http://dx.doi.org/10.1038/nphoton.2008.30 1749-4885 Google Scholar
M. W. Knightet al.,
“Photodetection with active optical antennas,”
Science, 332
(6030), 702
–704
(2011). http://dx.doi.org/10.1126/science.1203056 SCIEAS 0036-8075 Google Scholar
L. NovotnyN. van Hulst,
“Antennas for light,”
Nat. Photonics, 5 83
–90
(2011). http://dx.doi.org/10.1038/nphoton.2010.237 1749-4885 Google Scholar
C. FumeauxJ. AldaG. Boreman,
“Lithographic antennas at visible frequencies,”
Opt. Lett., 24
(22), 1629
–1631
(1999). http://dx.doi.org/10.1364/OL.24.001629 OPLEDP 0146-9592 Google Scholar
F. J. González,
“Thermal-impedance simulations of antenna-coupled microbolometers,”
Infrared Phys. Technol., 48
(3), 223
–226
(2006). http://dx.doi.org/10.1016/j.infrared.2005.10.003 IPTEEY 1350-4495 Google Scholar
A. CuadradoJ. GonzalezJ. Alda,
“Distributed bolometric effect in optical antennas and resonant structures,”
J. Nanophoton., 6
(1), 06351
(2012). http://dx.doi.org/10.1117/1.JNP.6.063512 JNOACQ 1934-2608 Google Scholar
C. Fumeauxet al.,
“Nanometer thin-film Ni-NiO-Ni diodes for detection and mixing of 30 THz radiation,”
Infrared Phys. Technol., 39
(3), 123
–183
(1998). http://dx.doi.org/10.1016/S1350-4495(98)00004-8 IPTEEY 1350-4495 Google Scholar
J. Eliasson,
“Metal-insulator-metal diodes for solar energy conversion,”
University of Colorado at Boulder,
(2001). Google Scholar
C. Fumeauxet al.,
“Measurement of the resonant lengths of infrared dipole antennas,”
Infrared Phys. Technol., 41
(5), 271
–281
(2000). http://dx.doi.org/10.1016/S1350-4495(00)00047-5 IPTEEY 1350-4495 Google Scholar
J. A. BeanB. A. SlovickG. D. Boreman,
“Influence of substrate configuration on the angular response pattern of infrared antennas,”
Opt. Express, 18
(21), 21705
–21713
(2010). http://dx.doi.org/10.1364/OE.18.021705 OPEXFF 1094-4087 Google Scholar
J.-S. Huanget al.,
“Impedance matching and emission properties of nanoantennas in an optical nanocircuit,”
Nano Lett., 9
(5), 1897
–1902
(2009). http://dx.doi.org/10.1021/nl803902t NALEFD 1530-6984 Google Scholar
F. Pelayo Garcia de Arqueret al.,
“Engineering the input impedance of optical nano dipole antennas: materials, geometry and excitation effect,”
IEEE Trans. Antennas Propag., 59
(9), 3144
–3153
(2011). http://dx.doi.org/10.1109/TAP.2011.2161544 IETPAK 0018-926X Google Scholar
I. WangY.-P. Du,
“Optical input impedance of nanostrip antennas,”
Opt. Eng., 51
(5), 054002
(2012). http://dx.doi.org/10.1117/1.OE.51.5.055002 OPEGAR 0091-3286 Google Scholar
A. CuadradoF. J. GonzálezJ. Alda,
“Material dependence of the distributed bolometric effect in resonant metallic nanostructures,”
Proc. SPIE, 8457 845724
(2012). http://dx.doi.org/10.1117/12.934124 PSISDG 0277-786X Google Scholar
J. Agustíet al.,
“An analytical model for the opto-thermo-mechanical conversion mechanisms in a MOEMS based energy harvester,”
Proc. SPIE, 8463 846313
(2012). http://dx.doi.org/10.1117/12.934828 PSISDG 0277-786X Google Scholar
A. Kovetz, The Principles of Electromagnetic Theory, Cambridge University Press, Cambridge, UK
(1990). Google Scholar
F. P. IncroperaD. P. DeWitt, Fundamentals of Heat and Mass Transfer, 4th ed.John Wiley & Sons, New York
(1996). Google Scholar
L. Novotny,
“Effective wavelength scaling for optical antennas,”
Phys. Rev. Lett., 28 266802
(2007). http://dx.doi.org/10.1103/PhysRevLett.98.266802 PRLTAO 0031-9007 Google Scholar
Handbook of Optical Constants of Solids, Academic Press, Orlando, Florida
(1985). Google Scholar
ASHRAE Handbook of Fundamentals, American Society of Heating, Refrigerating and Air Conditioning Engineers, ASHRAE, Washington, DC
(1993). Google Scholar
P. Lambkinet al.,
“Characterisation of CMOS compatible uncooled microbolometers,”
in IEEE Int. Conf. of Optical MEMS,
(2000). Google Scholar
X. XuA. MeadeY. Bayazitoglu,
“Numerical investigation of nanoparticle-assisted laser-induced interstitial thermotherapy toward tumor and cancer treatments,”
Laser Med. Sci., 26
(2), 231
–232
(2011). http://dx.doi.org/10.1007/s10103-010-0828-3 OPLEDP 0146-9592 Google Scholar
F. J. Gonzalezet al.,
“Thermal impedance model of electrostatic discharge effects on microbolometers,”
Microw. Opt. Techn. Lett., 26
(5), 291
–293
(2000). http://dx.doi.org/10.1002/(ISSN)1098-2760 MOTLEO 0895-2477 Google Scholar
Biography Alexander Cuadrado graduated in electronic engineering from the University of Basque Country, Bilbao, Spain, in 2010. He obtained his MS degree in photonics from the Universidad Autónoma de Madrid, in 2011. Currently he is working on his PhD dissertation at the University Complutense of Madrid, in the Applied Optics Complutense Group. He is researching the electromagnetic and thermal response of nanophotonic structures, focusing on the analysis of optical antennas, and in the characterization of MEMS devices that incorporate electromagnetically resonant elements.  Javier Alda graduated as a Lic. in sciences from the University of Zaragoza and received his PhD degree in physics from the University Complutense of Madrid in 1988. He joined the Optics Department of the University Complutense of Madrid in 1985 and he is currently professor of optics in this university. He has coauthored more than one hundred contributions as papers and book chapters, another one hundred communications to international meetings and conferences, and he had three patents in optics. He has been visiting researcher at the University of Central Florida, Stanford University, and Universidad Autónoma de San Luis Potosí, totaling more than three years. His main research interest is in the wide area of Applied Optics, with special emphasis in the analysis and characterization of optical antennas and resonant optics. He is member of the International Society for Optical Engineering, the European Optical Society, and the Optical Society of America.  Francisco Javier González received the BS degree in electrical engineering from ITESO University, Guadalajara, Mexico, in 1996, and the MS and PhD degrees in electrical engineering from the School of Optics and Photonics, University of Central Florida, Orlando, in 2000 and 2003, respectively. He was a research assistant and later a research scientist at the Infrared Systems Lab, School of Optics and Photonics, Orlando, FL. He is currently a professor at the Autonomous University of San Luis Potosí, San Luis Potosi, Mexico. He has been a visiting scholar at the University Complutense of Madrid, the University of Central Florida and the University of Notre Dame. He has authored or coauthored more than 45 journal papers, and holds three patents in the areas of infrared detectors, nanophotonics, and biomedical applications of physics and optics. Currently his research interests are in the areas of nanophotonics and biophotonics. He is a member of the Mexican Academy of Sciences, the International Society for Optical Engineers, and the American Institute of Physics and Senior Member of the Institute of Electrical and Electronics Engineers. |