|
|
|
A thin light beam, such as that emitted by a laser, may possess a hidden rotational structure, invisible to the naked eye. This structure is rooted in the electromagnetic wave nature of light and it takes two distinct forms, which may be dubbed spin and twist. Spin is associated with the rotation of the electric and magnetic fields oscillating within the optical wave—i.e., the circular polarization of light. Twist instead occurs in light waves having a helical-shaped (or twisted) wavefront and an optical vortex located at the beam axis. When a free material particle absorbs light having spin or twist, it is itself made to spin—in other words, the light exerts a rotational form of radiation pressure, showing that this kind of light carries angular momentum. More specifically, the angular momentum of light having circular polarization is named as spin angular momentum (SAM), while that associated with a spiral wavefront is called orbital angular momentum (OAM). The OAM of light has recently been attracting much attention for its possible technological applications in the areas of particle manipulation, optical sensing, and classical and quantum optical communication. While different methods exist for generating light with spin or twist separately, until 2006 there was no known way to couple these two forms of rotation to each other. In 2006, the introduction of the device named -plate provided scientists with a tool to couple spin and twist and make them interact, allowing, e.g., to use one to control the other or vice versa.1 In suitable conditions, this process even leads to an exact conversion of the angular momentum from the SAM form to the OAM form within the same light beam, without any angular momentum exchange with external bodies. More generally, the -plate is capable of imparting OAM to a light beam by exploiting a variation of SAM. This allows, e.g., the generation of light having OAM starting with ordinary light (with zero OAM) having circular polarization. The -plate is a liquid crystal cell, essentially a thin liquid crystal film sandwiched between two glasses, with a peculiar singular pattern of molecular alignment, obtained by a suitable previous treatment of the containing glass surfaces (see Fig. 1). The pattern is mainly defined by a characteristic number, named topological charge and characterizing the central singularity, that is usually denoted by the mathematical symbol , from which the device took its name.2 In addition, as the optical effect of liquid crystal can be controlled electrically, the -plates can be tuned for having a partial effect, if desired, or even switched on and off.3 Since its first introduction, the -plate has found a number of interesting applications in classical and quantum photonics. Fig. 1A -plate device with topological charge and electric tuning, as seen between crossed polarizers, thus revealing the (otherwise invisible) singular birefringent pattern. Photo by Sergei Slussarenko.  Classically, the -plate has been mainly used for generating light beams with nonzero OAM in a controlled way (see Fig. 2). Compared to other methods for generating OAM (such as spiral phase plates and holographic elements), the -plates have some practical advantages: they are thin optical elements working in transmission, with high transmission efficiency and inducing no light deflection in the transmitted beam; they are electrically controlled, as already explained; the OAM sign (i.e., the direction of rotation) is controlled by that of the input polarization (the SAM sign). The latter, in particular, is a very important feature for possible communication applications, because the polarization can be switched very fast with electro-optical devices, and for quantum information applications, as we will discuss further below. Fig. 2Schematics of the optical effect of a -plate. Left (right) circularly polarized light having zero OAM at the input is converted into light carrying an OAM per photon given by . The circular polarization handedness gets also inverted in the process. 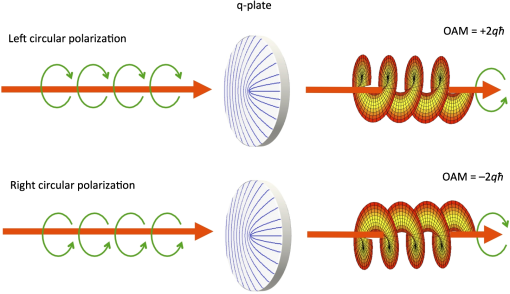 More recently, the -plates have been used for generating vector vortex beams and polarization-singular beams,4,5 which are two classes of light beams with nonuniform transverse polarization patterns, of interest in singular optics. These beams can be seen as superpositions of two waves having different OAMs and different uniform polarizations, and they are generated very simply with -plates by using the input light with elliptical or linear polarization and by properly adjusting the -plate electric tuning. Since the induced OAM sign of the -plate output is controlled by the sign of the input light polarization, quantum superpositions of positive and negative OAM values can be easily obtained from polarization superpositions, which in turn are easily prepared using only conventional optics. Quantum superpositions of two distinct physical states define the qubits, the elementary units of quantum information. Typically, photons—the elementary particles of light—are used as a carrier of qubits for applications in quantum information, particularly quantum communication. A -plate can be used for transferring qubits initially encoded in polarization to the OAM of a photon and vice versa. This quantum process was first demonstrated in 2009,6 and it allowed the implementation of simple quantum-information tasks in OAM, such as the optimal quantum cloning of an OAM qubit (i.e., making the best possible copy of the input qubit which is allowed by the laws of quantum mechanics) from one photon to another.7 The obvious subsequent step has then been that of storing multiple qubits in each photon, by using both the polarization and the OAM, and demonstrating again tasks such as the optimal quantum cloning.8 Another very recent application of the -plate has been that of generating light beams or even individual photons with tailored sensitivity to rotation. First, photons that are fully insensitive to rotations around the beam axis were generated—i.e., fully rotation-symmetric—and used for demonstrating the possibility of transmitting quantum information without the need to align the reference frames of the transmitting and receiving units.9 In the future, this feature might be an important element of satellite-based world-wide networks for distributing secret keys using quantum cryptography. Next, the opposite effect has been obtained, i.e., photons that are extremely sensitive to rotations. This result, exploiting -plates with very large values of the topological charge , allowed demonstrating the photonic polarization-gear device, that gives rise to a very large rotation of the optical polarization plane (i.e., the plane in which the wave electric field oscillates) in the output light as a consequence of a very small mechanical rotation.10 The most obvious application of this effect is for measuring mechanical rotations with very high precision in a noncontact way. Various other developments of the optics research relying on -plates can be foreseen for the next few years. In the classical optics domain, the possibility of writing more complex patterns in the liquid crystal structure could give rise to new optical functionalities, enabling, e.g., the generation of more complex structured light beams, possibly useful for particle manipulation, or for optimized applications in optical coronagraphy. Other possibilities are the simultaneous generation of arrays of optical vortices or the creation of new optical device concepts based on suitable sequences of -plates. As few-mode optical fibers become more attractive for large-bandwidth optical communication, by exploiting the emerging technologies of space-division multiplexing, the -plates devices could become important photonic elements to address different spatial modes in a direct way, couple them together during propagation, or to couple them to free-space external modes. In the quantum optics domain, the possibility of encoding an increasing number of qubits per photon may allow significant progress in quantum communication and, possibly, even in small-scale quantum computation. Quantum walks in the space of OAM could supplement other methods for performing the quantum simulations that are mimicking other more complex quantum systems in a perfectly controlled setting. Finally, new possibilities for quantum information storage or quantum processing may arise from exploiting the interaction of light carrying OAM with trapped cold atoms or with hybrid light-matter systems, such as Bose–Einstein condensates of exciton polaritons in semiconductor microcavities. ReferencesL. MarrucciC. ManzoD. Paparo,
“Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media,”
Phys. Rev. Lett., 96
(16), 163905
(2006). http://dx.doi.org/10.1103/PhysRevLett.96.163905 PRLTAO 0031-9007 Google Scholar
S. Slussarenkoet al.,
“Tunable liquid crystal -plates with arbitrary topological charge,”
Opt. Express, 19
(5), 4085
–4090
(2011). http://dx.doi.org/10.1364/OE.19.004085 OPEXFF 1094-4087 Google Scholar
B. Piccirilloet al.,
“Photon spin-to-orbital angular momentum conversion via an electrically tunable -plate,”
Appl. Phys. Lett., 97
(24), 241104
(2010). http://dx.doi.org/10.1063/1.3527083 APPLAB 0003-6951 Google Scholar
F. Cardanoet al.,
“Polarization pattern of vector vortex beams generated by -plates with different topological charges,”
Appl. Opt., 51
(10), C1
–C6
(2012). http://dx.doi.org/10.1364/AO.51.0000C1 APOPAI 0003-6935 Google Scholar
F. Cardanoet al.,
“Generation and dynamics of optical beams with polarization singularities,”
Opt. Express, 21
(7), 8815
–8820
(2013). http://dx.doi.org/10.1364/OE.21.008815 OPEXFF 1094-4087 Google Scholar
E. Nagaliet al.,
“Quantum information transfer from spin to orbital angular momentum of photons,”
Phys. Rev. Lett., 103
(1), 013601
(2009). http://dx.doi.org/10.1103/PhysRevLett.103.013601 PRLTAO 0031-9007 Google Scholar
E. Nagaliet al.,
“Optimal quantum cloning of orbital angular momentum photon qubits through Hong-Ou-Mandel coalescence,”
Nat. Photon., 3
(12), 720
–723
(2009). http://dx.doi.org/10.1038/nphoton.2009.214 1749-4885 Google Scholar
E. Nagaliet al.,
“Experimental optimal cloning of four-dimensional quantum states of photons,”
Phys. Rev. Lett., 105
(7), 073602
(2010). http://dx.doi.org/10.1103/PhysRevLett.105.073602 PRLTAO 0031-9007 Google Scholar
V. D’Ambrosioet al.,
“Complete experimental toolbox for alignment-free quantum communication,”
Nat. Commun., 3 961
(2012). http://dx.doi.org/10.1038/ncomms1951 NCAOBW 2041-1723 Google Scholar
V. D’Ambrosioet al.,
“Photonic polarization gears for ultra-sensitive angular measurements,”
Nat. Commun., 4 2432
(2013). http://dx.doi.org/10.1038/ncomms3432 NCAOBW 2041-1723 Google Scholar
|

