|
|
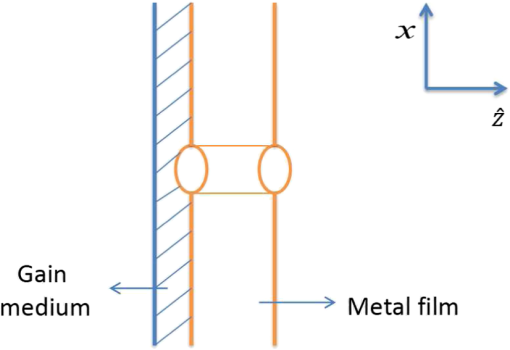
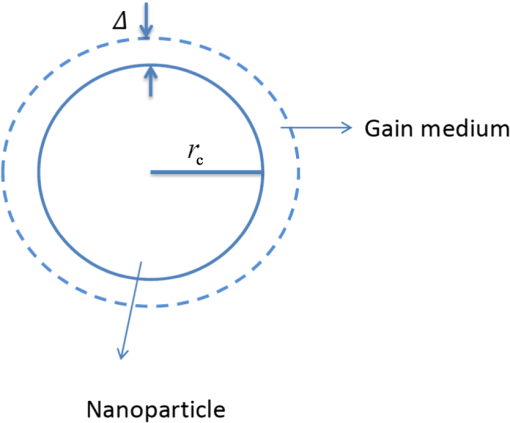
1.IntroductionThe surface plasma wave (SPW), supported by a conductor–dielectric interface, has an important property: as the wave frequency approaches the surface plasmon resonance, the wavelength and transverse extent of the mode resonantly shrink, confining optical frequency waves to nanodimensions, far below the diffraction limit prescribed for body waves.1,2 This has led to the development of nanoelectronics and nano-devices into a major field1–5 of research. Of significant importance is the development of nanolaser or spaser.6–10 Noginov et al.11 have recently operated a 531 nm spaser-based nanolaser employing 44 nm diameter nanoparticles with gold core and dye-doped silica shell. Lu et al.12,13 have developed a multilayer plasminic nanolaser using smooth silver film with or nanolayer and gallium nitride nanorod deposited on it. The nanorod comprises a layer of indium gallium nitride that acts as gain medium. The theoretical formalisms of spaser are usually based on quantum density matrix approach.6 However, some employ classical model due to its transparent simplicity. Kumar et al.14 developed a classical analytical formalism of two-layer surface plasmon laser amplifier pumped by a forward biased p–n junction. In this paper, we present theoretical analysis of optical gain in three surface plasmonic nano-oscillators, (i) a metal film with a nanostrip of gain medium, (ii) a nanohole in a metal film deposited on a gain layer,15 and (iii) a nanoparticle coated with gain medium. These are the configurations experimentally studied in recent years and have promise for building arrays of nanoradiators with desired directivity and power. Here we pursue analytical treatment to reveal physics with some clarity which at times gets masked in numerical simulations. The oscillators operate near the surface plasmon resonance frequency and the quality factor of the cavity is determined by the free electron collisional damping. In the first oscillator, nanostrip provides for lateral localization of the surface plasmons16 by reducing the phase velocity of the SPW (as compared to the metal–vacuum interface). In the second oscillator, mode is localized around the nanohole. In the third case, space charge oscillations of electron sphere with respect to ion sphere provide a natural oscillator. The field of the oscillator mode stimulates electron–hole recombination in the gain medium that in turn amplifies the mode. In Sec. 2, we study the optical gain in a metal-nanostrip oscillator. In Secs. 3 and 4, we consider the nanohole and nanoparticle oscillators. In Sec. 5, we discuss the results. 2.Metal Film—Nanostrip SpaserConsider a metal film of free electron density , electron effective mass , and lattice dielectric constant . On top of it () lies a nanostrip with , and dielectric constant (cf. Fig. 1). The thickness of the metal film is larger than the skin depth of the SPW, hence it can be treated like a semi-infinite medium (). Grooves are created in the metal at , for longitudinal localization of plasmons. Fig. 1Schematic of nanostrip-loaded metal film. The nanostrip of length , width , and relative permittivity localizes the SPW. It contains a layer of gain medium that under optical pumping excites localized surface plasmons. 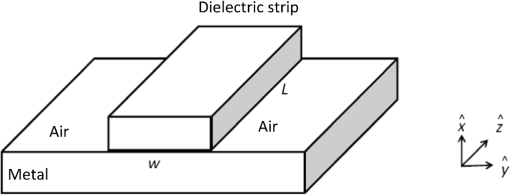 Had it been an infinite metal–dielectric interface, it would support a SPW with electric field17 where , , is the effective relative permittivity of the metal, is the plasma frequency, is the electron charge, is the electron collision frequency, is the free space permittivity. SPW exists for whereFor a given , increases with increasing . When one limits the lateral size of the dielectric layer, the parallel wave number of the SPW on the metal–vacuum interface is One may take the SPW to be propagating along but with finite . Outside the strip, i.e., on the metal–vacuum interface, the SPW would have the same as inside the strip. However, since , the SPW field outside the strip would be evanescent in . One may take SPW to be localized in and with where and are integers.For the plasmon nano-oscillator, we may deduce the mode structure as follows. Take , . Assuming , variations of fields as and using and express , , , in terms of . In different regions one may take the , variations of fields to be the same [with , given by Eq. (5)], in compliance with the boundary conditions at and allow to have different values in different media. Thus we write in the region , Applying the continuity of , at , we obtain and the dispersion relation giving as in Eq. (2). Since is quantized [cf. Eq. (5)], we get discrete eigenfrequencies . In the absence of collisions (), is real and so are the frequencies. For , has a finite imaginary part, . Writing , we obtain where . We have plotted in Fig. 2(a) the real frequency of a surface plasmon eigenmode as a function of normalized width of the strip for typical parameters. The frequency steadily falls off with the width. Figure 2(b) displays the variation of normalized damping rate with normalized frequency. The damping increases rather rapidly as one approaches the surface plasmon resonance frequency.Fig. 2(a) Normalized eigenfrequency of the plasmon oscillator as a function of normalized width of the strip for , , , , . (b) Normalized damping rate as a function of normalized frequency for , , . 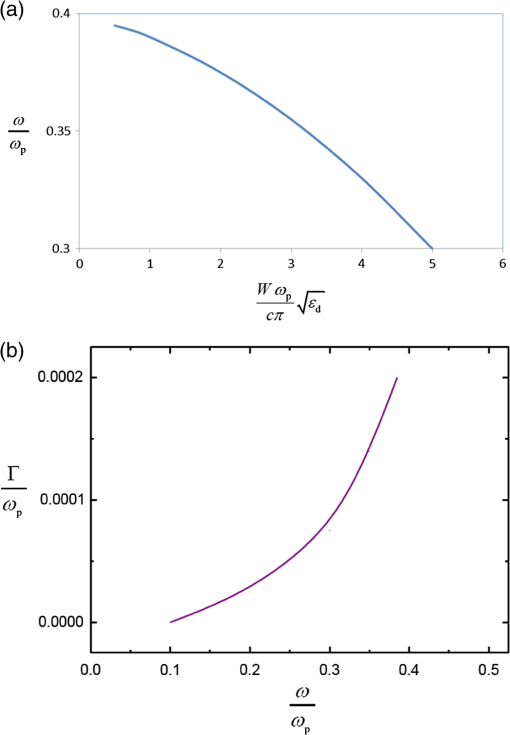 The energy density of the electromagnetic fields of the plasmon resonator is where for , for . The total energy stored in the SPW is2.1.Optical GainNow we allow the dielectric strip to comprise a gain medium (e.g., an optically pumped semiconductor layer) of -width , -width , and -extent , located at . In the conduction and valence bands, the density of states and occupation probability for electrons and holes (of effective masses , ), respectively, are where and are the electron and hole energies measured from the bottom of the conduction band upward and top of the value band downward, respectively, and are the Fermi energies related to electron and hole densities and and temperature (in energy units).In a surface plasmon-induced emission process, an electron in energy state in the conduction band goes to energy state in the valence band, recombining with a hole and producing a plasmon of frequency where is the band gap. The vector of the plasmon is much smaller than that of the electron before or after the transition, hence in a direct band gap parabolic band semiconductor we may takeEquations (15) and (16) give the energy states that participate in the stimulated emission process The rate of e–h recombination per unit volume per second is proportional to spectral energy density , density of states , the occupation probability of state , the probability of state being vacant, where is the Einstein’s coefficient of stimulated emission and is the eigenfrequency of the SPW mode. Similarly, the rate of transition of electrons from the valence band to conduction band per unit volume per second isOne may remember that is proportional to the density of states in the valence band . The net SPW energy produced per unit volume per second on integrating over is where we have dropped the subscript m over . Integrating it over the volume of the gain medium, we obtain the rate of energy gain by the SPW oscillatorUsing Eqs. (12) and (21) we obtain is the growth rate of SPW field energy. The threshold for the SPW growth is given as This determines the electron and hole density threshold for the growth of surface plasmons. The Einstein’s coefficient is related to the Einstein’s coefficient for spontaneous emission as , hence which is of the order of . Typical value of , the inverse e–h recombination time, is . Further, for spaser operating around , , . For silver, gallium nitride case , . Thus, when the occupation probabilities and are just greater than 0.5 each the threshold for the spaser is exceeded and the growth rate of the order of is achieved.3.Nanohole-Embedded Metal Film SpaserConsider a metal film of thickness () and effective relative permittivity given above. It comprises a transverse hole of radius and length with vacuum inside (cf. Fig. 3). The cylindrical vacuum–metal interface supports an SPW with evanescent fields in and forward backward propagating solutions in . A forward wave SPW field is where , and , , , are the modified Bessel functions. The continuity of , at gives the dispersion relationThe termination of the cylinder at , quantizes and gives standing wave solution to SPW. One may write with and for the fundamental mode. The dispersion relation, Eq. (26), gives the eigenfrequency and damping rate of the SPW mode.The energy density of fields of the plasmon nano-oscillator is The total energy stored in the SPW is3.1.Optical GainWe allow a thin layer of gain medium of thickness placed at . The net SPW energy produced per unit volume per second, , is given by Eq. (20). The rate of energy gain of the SPW oscillator is given by Eq. (21) with The linear damping rate is of the order of the one given by Eq. (10). Equation (21) gives with growth rate The threshold value of above which the SPW grows is obtained by putting in Eq. (32). Above the threshold the growth rate is comparable to the earlier case. 4.Nanoparticle SpaserConsider a metallic nanoparticle of radius , free electron density , electron effective mass , and lattice permittivity . It is surrounded by a layer of gain medium of thickness and dielectric constant (cf. Fig. 4). For a moment, let us take and give a displacement to free electrons of the nanoparticles. This creates a space charge field in the overlap region of the free electron sphere and ion sphere. Each electron thus experiences a restoration force , where . The momentum loss per electron per second via collisions is where ν is the collision frequency and is the drift velocity of electrons. Thus the equation of motion for an electron is18 Presuming a solution we get giving , where we have assumed . Thus the nanoparticle is a natural oscillator of frequency and quality factor .When we allow to have arbitrary value, the Poisson’s equation, governing the space charge field , on writing , gives the solution (for ) Demanding the continuity of , at we obtain Using the value of given below Eq. (2), we obtain the frequency given by Eq. (35) with replaced by . This is the same result obtained by Bergman and Stockman19 and Noginov et al.20 for the fundamental mode. The field of the nanoparticle [of dipole moment ] as seen by the gain layer is Outside the gain layer () the field is given by the above expression with replaced by 1. The energy stored in the oscillator is where the volume integration has been carried out from inside the particle to the entire outside.The oscillator field induces e–h recombination producing electromagnetic energy per second as given by Eq. (21) with given by Eq. (35) and The growth rate of the SPW turns out to be For , , and , . One percent above the 50% occupation probability, the growth rate . 5.DiscussionThe surface plasmon eigenmode in the vicinity of SPW resonance, is strongly localized near the metal–dielectric interface with and has resonantly short wavelength. The damping rate of the mode, however, shows no resonant enhancement. A gain medium, within an SPW wavelength from the boundary sustaining SPW, excites the SPW eigenmode. Usually one employs optical pumping to achieve , the condition equivalent of population inversion. For electron and hole occupation probabilities of relevant energy states in the conduction and valence bands exceeding 0.5 each by 1% the growth rate is of the order of . In the case of metal film loaded with a gain medium nanostrip, frequency can be tuned by varying the permittivity and width of the strip. A drastic reduction in operating frequency can be achieved by shrinking the thickness of the metal film that lowers the SPW resonance frequency.21 However, the present analysis is not valid in that case. The nanohole oscillator has a gain comparable to the above oscillator at the same level of pumping power flux density. The SPW eigenmode acts as an oscillating dipole and emits far-field radiation. An array of such holes would give a well-collimated beam. The oscillator comprising a nanoparticle coated with an optically pumped gain medium has operating frequency independent of the radius of the particle. It depends only on its free carrier density, lattice permittivity, and dielectric constant of the surrounding medium. Noginov et al.20 have reported compensation of loss in metal nanoparticles oscillator by gain in interfacing rhodemine 6G dye. With emission cross section of R6G and density of active molecules (corresponding to one molecule per nanoparticles of radius 5 nm) the local gain turns out to be , corresponding to temporal growth which is comparable to our case where e–h recombination leads to growth of plasmons when , i.e., . The quality factor of the oscillators estimated here due to collisional losses appears to be higher than that reported experimentally. Photoabsorption via interband transitions appears to dominate collisional losses. These losses are equivalent to enhanced collision frequency of electrons. ReferencesW. L. Burnes, A. Dereux and T.W. Ebbesen,
“Surface plasmon subwavelength optics,”
Nature, 424
(6950), 824
–830
(2003). http://dx.doi.org/10.1038/nature01937 Google Scholar
S. I. Bozhevolnyi et al.,
“Channel plasmon subwavelength waveguide components including interferometers and ring resonators,”
Nature, 440
(7083), 508
–511
(2006). http://dx.doi.org/10.1038/nature04594 Google Scholar
H. A. Atwater and A. Polman,
“Plasmonics for improved photovoltaic devices,”
Nat. Matter., 9
(3), 205
–213
(2010). http://dx.doi.org/10.1038/nmat2629 Google Scholar
X. D. Hoa, A. G. Kirk and M. Tabrizian,
“Towards integrated and sensitive surface plasmon resonance biosensors: a review of recent progress,”
Biosens. Bioelectr., 23
(2), 151
–160
(2007). http://dx.doi.org/10.1016/j.bios.2007.07.001 BBIOE4 0956-5663 Google Scholar
Z. Wu et al.,
“Long range surface plasmon devices design using subwavelength metal grating,”
J. Nonlinear Opt. Phys. Matter., 17
(4), 413
–423
(2008). http://dx.doi.org/10.1142/S0218863508004329 Google Scholar
M. I. Stockman,
“The spaser as a nanoscale quantum generator and ultrafast amplifier,”
J. Opt., 12
(1), 024004
(2010). http://dx.doi.org/10.1088/2040-8978/12/2/024004 Google Scholar
P. Berini and I. De Leon,
“Surface plasmon-polariton amplifiers and lasers,”
Nat. Photonics, 6
(1), 16
–24
(2012). http://dx.doi.org/10.1038/nphoton.2011.285 Google Scholar
R. M. Ma et al.,
“Room-temperature sub-diffraction-limited plasmon laser by total internal reflection,”
Nat. Matter., 10
(2), 110
–113
(2011). http://dx.doi.org/10.1038/nmat2919 Google Scholar
T. P. H. Sidiropoulos et al.,
“Ultrafast plasmonic nanowire lasers near the surface plasmon frequency,”
Nat. Phys., 10
(11), 870
–876
(2014). http://dx.doi.org/10.1038/nphys3103 Google Scholar
K. Unterrainer et al.,
“Quantum cascade lasers with double metal-semiconductor waveguide resonators,”
Appl. Phys. Lett., 80
(17), 3060
–3062
(2002). http://dx.doi.org/10.1063/1.1469657 APPLAB 0003-6951 Google Scholar
M. A. Noginov et al.,
“Demonstration of a spaser-based nanolaser,”
Nat. Lett., 460
(7259), 1110
–1112
(2009). http://dx.doi.org/10.1038/nature08318 Google Scholar
Y. J. Lu et al.,
“Plasmonic nanolaser using epitaxially grown silver film,”
Science, 337
(6093), 450
–453
(2012). http://dx.doi.org/10.1126/science.1223504 SCIEAS 0036-8075 Google Scholar
Y. J. Lu et al.,
“All-color plasmonic nanolasers with ultralow thresholds: autotuning mechanism for single-mode lasing,”
Nano Lett., 14
(8), 4381
–4388
(2014). http://dx.doi.org/10.1021/nl501273u NALEFD 1530-6984 Google Scholar
P. Kumar, V. K. Tripathi and C. S. Liu,
“A surface plasmon laser,”
J. Appl. Phys., 104
(3), 033306
(2008). http://dx.doi.org/10.1063/1.2952018 JAPIAU 0021-8979 Google Scholar
F. van Beijnum et al.,
“Surface plasmon lasing observed in metal hole arrays,”
Phys. Rev. Lett., 110
(20), 206802
(2013). http://dx.doi.org/10.1103/PhysRevLett.110.206802 PRLTAO 0031-9007 Google Scholar
T. Holmgaard and S. I. Bozhevolnyi,
“Theoretical analysis of dielectric-loaded surface plasmon-polariton waveguides,”
Phys. Rev. B, 75
(24), 245405
(2007). http://dx.doi.org/10.1103/PhysRevB.75.245405 Google Scholar
C. S. Liu and V. K. Tripathi, Electromagnetic Theory for Telecommunications, Foundation BooksCambridge University Press India Pvt. Ltd., Delhi
(2007). Google Scholar
M. Kumar and V. K. Tripathi,
“Rayleigh scattering of a Gaussian laser beam from expanding clusters,”
Phys. Plasmas, 16
(12), 123111
(2009). http://dx.doi.org/10.1063/1.3274927 PHPAEN 1070-664X Google Scholar
D. J. Bergman and M. I. Stockman,
“Surface plasmon amplification by stimulated emission of radiation: quantum generation of coherent surface plasmons in nanosystems,”
Phys. Rev. Lett., 90
(2), 027402
(2003). http://dx.doi.org/10.1103/PhysRevLett.90.027402 PRLTAO 0031-9007 Google Scholar
M. A. Noginov et al.,
“The effect of gain and absorption on surface plasmons in metal nanoparticles,”
Appl. Phys. B, 86
(3), 455
–460
(2007). http://dx.doi.org/10.1007/s00340-006-2401-0 Google Scholar
P. Kumar and V. K. Tripathi,
“Terahertz surface plasmons excitation by nonlinear mixing of lasers in over ultrathin metal film coated dielectric,”
J. Appl. Phys., 114
(5), 053101
(2013). http://dx.doi.org/10.1063/1.4817091 JAPIAU 0021-8979 Google Scholar
BiographyChuan S. Liu is a leading plasma physicist, credited with groundbreaking contributions to theory of laser plasma interaction and promoting international collaboration in higher education. He joined the University of Maryland in 1975 as professor of physics and served twice as department chair. He also served as vice president for research and dean of the graduate school. From 2003 to 2006, he was president of National Central University, Taiwan. Currently, he is the founding master of the Chao Kuang Piu College. Vipin K. Tripathi received his master’s in physics from Agra University in 1967 and a PhD from IIT Delhi in 1971. In 1972, he joined the IIT faculty. In 1976, he moved to the University of Maryland and worked in the area of thermonuclear fusion, developing nonlinear theories of RF heating and current drive in tokamak. In 1983, he joined IIT Delhi as professor of physics. He established a leading group in free electron laser and laser plasma interaction. |